
【题目】百年大计,教育为本.某校积极响应教育部号召,不断加大拔尖人才的培养力度,为清华、北大等排名前十的名校输送更多的人才.该校成立特长班进行专项培训.据统计有如下表格.(其中![]() 表示通过自主招生获得降分资格的学生人数,
表示通过自主招生获得降分资格的学生人数,![]() 表示被清华、北大等名校录取的学生人数)
表示被清华、北大等名校录取的学生人数)
年份(届) | 2014 | 2015 | 2016 | 2017 | 2018 |
| 41 | 49 | 55 | 57 | 63 |
| 82 | 96 | 108 | 106 | 123 |
(1)通过画散点图发现![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(保留两位有效数字)
的线性回归方程;(保留两位有效数字)
(2)若已知该校2019年通过自主招生获得降分资格的学生人数为61人,预测2019年高考该校考人名校的人数;
(3)若从2014年和2018年考人名校的学生中采用分层抽样的方式抽取出5个人回校宣传,在选取的5个人中再选取2人进行演讲,求进行演讲的两人是2018年毕业的人数![]() 的分布列和期望.
的分布列和期望.
参考公式: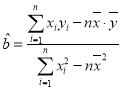 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】将编号为1,2,3,4,5,6,7的小球放入编号为1,2,3,4,5,6,7的七个盒子中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为( ).
A.5040B.24C.315D.840
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某精密仪器生产车间每天生产![]() 个零件,质检员小张每天都会随机地从中抽取50个零件进行检查是否合格,若较多零件不合格,则需对其余所有零件进行检查.根据多年的生产数据和经验,这些零件的长度服从正态分布
个零件,质检员小张每天都会随机地从中抽取50个零件进行检查是否合格,若较多零件不合格,则需对其余所有零件进行检查.根据多年的生产数据和经验,这些零件的长度服从正态分布![]() (单位:微米
(单位:微米![]() ),且相互独立.若零件的长度
),且相互独立.若零件的长度![]() 满足
满足![]() ,则认为该零件是合格的,否则该零件不合格.
,则认为该零件是合格的,否则该零件不合格.
(1)假设某一天小张抽查出不合格的零件数为![]() ,求
,求![]() 及
及![]() 的数学期望
的数学期望![]() ;
;
(2)小张某天恰好从50个零件中检查出2个不合格的零件,若以此频率作为当天生产零件的不合格率.已知检查一个零件的成本为10元,而每个不合格零件流入市场带来的损失为260元.假设![]() 充分大,为了使损失尽量小,小张是否需要检查其余所有零件,试说明理由.
充分大,为了使损失尽量小,小张是否需要检查其余所有零件,试说明理由.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足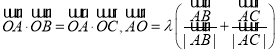 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.
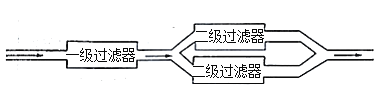
其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图
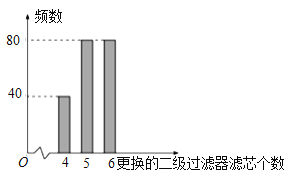
以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列结论正确的个数有( )
,则下列结论正确的个数有( )
①![]() 是函数
是函数![]() 图像的一条对称轴
图像的一条对称轴
②![]() 是函数
是函数![]() 图像的一个对称中心
图像的一个对称中心
③将函数![]() 图像向右平移
图像向右平移![]() 单位所得图像的解析式为得
单位所得图像的解析式为得![]()
④函数![]() 在区间
在区间![]() 内单调递增
内单调递增
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知函数![]() 是奇函数,
是奇函数,![]() 的定义域为
的定义域为![]() .当
.当![]() 时,
时,![]()
![]() .(e为自然对数的底数).
.(e为自然对数的底数).
(1)若函数![]() 在区间
在区间![]() 上存在极值点,求实数
上存在极值点,求实数![]() 的取值范围;
的取值范围;
(2)如果当x≥1时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com