
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4和最小值1.设
上有最大值4和最小值1.设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=ln ![]() 的图象分别与直线y=m交于A,B两点,则|AB|的最小值为( )
的图象分别与直线y=m交于A,B两点,则|AB|的最小值为( )
A.2
B.2+ln2
C.e2 ![]()
D.2e﹣ln ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,满足x2+y2≤1,x≥0,y≥0的点P(x,y)的集合对应的平面图形的面积为 ![]() ;类似的,在空间直角坐标系O﹣xyz中,满足x2+y2+z2≤1,x≥0,y≥0,z≥0的点P(x,y,z)的集合对应的空间几何体的体积为( )
;类似的,在空间直角坐标系O﹣xyz中,满足x2+y2+z2≤1,x≥0,y≥0,z≥0的点P(x,y,z)的集合对应的空间几何体的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中
,其中 ![]() =(2cosx,
=(2cosx, ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R
=(cosx,1),x∈R
(1)求函数y=f(x)的最小正周期和单调递增区间:
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=2,a= ![]() 且sinB=2sinC,求△ABC的面积.
且sinB=2sinC,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a和b的值.
(2)说明函数g(x)的单调性;若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
(3)设 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |
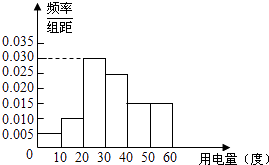
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种. 
A.21
B.32
C.43
D.54
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com