考点:三角函数的和差化积公式,三角函数的积化和差公式
专题:证明题,三角函数的求值
分析:(1)积化和差公式是由正弦或余弦的和角公式与差角公式通过加减运算推导而得.
(2)有了(1)积化和差的公式以后,我们只需一个变形,就可以得到和差化积的公式.我们把上述公式中的α+β设为θ,α-β设为φ,那么α=
(θ+φ),β=
(θ-φ),把α,β分别用θ,φ表示就可以得到和差化积的四个公式.
解答:
解:(1)①∵sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,
∴把两式相减,得到:cosαsinβ=
[sin(α+β)-sin(α-β)],
②∵cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,
∴把两式相加,得到:cos(α+β)+cos(α-β)=2cosαcosβ,
∴所以,cosαcosβ=
[cos(α+β)+cos(α-β)],
③∴同理,两式相减,得到sinαsinβ=-
[cos(α+β)-cos(α-β)];
(2)把上述公式中的α+β设为θ,α-β设为φ,那么α=
,β=
,把α,β分别用θ,φ表示就可以得到和差化积的公式:
①∵由(1)得cosαsinβ=
[sin(α+β)-sin(α-β)],
∴cos
sin
=
[sinθ-sinφ],
∴sinθ-sinφ=2cos
sin
,
②∵由(1)得cosαcosβ=
[cos(α+β)+cos(α-β)],
∴cos
cos
=
[cosθ+cosφ],
∴cosθ+cosφ=2cos
cos
,
③∵由(1)得sinαsinβ=-
[cos(α+β)-cos(α-β)],
∴sin
sin
=-
[cosθ-cosφ],
∴cosθ-cosφ=-2sin
sin
.
点评:本题主要考查了三角函数的和差化积公式,三角函数的积化和差公式的证明,考查了转化思想,属于基本知识的考查.



 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案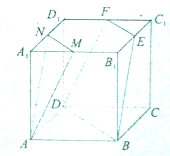 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点. 如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=
如图,已知F是菱形ABCD的对角线的交点,平面ABCD⊥平面DEC,ED=