
【题目】如图,已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,离心率为
,离心率为![]() .
.
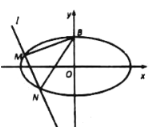
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭园C交于
与椭园C交于![]() ,
,![]() 两点,直线
两点,直线![]() 与线
与线![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过定点,并求
过定点,并求![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() 的面积
的面积![]() 的最大值
的最大值![]() .
.
【解析】
(1)求出![]() 后可得椭圆的方程.
后可得椭圆的方程.
(2)设MN:y=kx+m,M(x1,y1),N(x2,y2),与椭圆方程联立化为(1+4k2)x2+8kmx+4m2﹣4=0,△>0.由kBMkBN![]()
利用根与系数的关系代入化简可得:m2+2m﹣3=0,解得m.再求得|MN|,点B到直线MN的距离d,可得S△BMN,通过换元利用基本不等式的性质即可得出.
(1)因为一个顶点为![]() ,故
,故![]() ,又离心为
,又离心为![]() ,故
,故![]() 即
即![]() ,
,
所以![]() ,故椭圆方程为:
,故椭圆方程为:![]() .
.
(2)若直线![]() 的斜率不存在,则设
的斜率不存在,则设![]() ,
,![]()
此时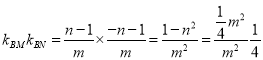 ,与题设条件矛盾,故直线
,与题设条件矛盾,故直线![]() 的斜率必存在.
的斜率必存在.
设MN:y=kx+m,M(x1,y1),N(x2,y2),
联立![]() ,化为(1+4k2)x2+8kmx+4m2﹣4=0,
,化为(1+4k2)x2+8kmx+4m2﹣4=0,
△=16(4k2﹣m2+1)>0,
∴x1+x2![]() ,∴x1x2
,∴x1x2![]() .
.
∵kBMkBN![]()
∴![]() x1x2+k(m﹣1)(x1+x2)+(m﹣1)2=0,
x1x2+k(m﹣1)(x1+x2)+(m﹣1)2=0,
∴![]() k(m﹣1)
k(m﹣1)![]() (m﹣1)2=0,
(m﹣1)2=0,
化为m2+2m﹣3=0,解得m=﹣3或m=1(舍去).
即直线过定点(0,﹣3)
∴|MN|![]()
![]()
点B到直线MN的距离d![]() .
.
∴S△BMN![]() MNd
MNd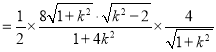 .
.
由m=﹣3,△>0,可知:k2﹣2>0,令![]() t>0,
t>0,
∴k2=t2+2,
∴S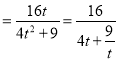 ,当且仅当t
,当且仅当t![]() ,即k=±
,即k=±![]() 时,Smax
时,Smax![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费对年销售量(单位:t)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费x(万元)和年销售量y(单位:t)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.

(1)根据表中数据建立年销售量y关于年宣传费x的回归方程;
(2)已知这种产品的年利润z与x,y的关系为![]() ,根据(1)中的结果回答下列问题:
,根据(1)中的结果回答下列问题:
①当年宣传费为10万元时,年销售量及年利润的预报值是多少?
②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.
附:回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为

参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 是等边三角形,且平面
是等边三角形,且平面![]()
![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
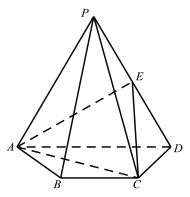
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. “![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C. 命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”
”
D. “若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题
”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,且满足
,且满足![]() .
.
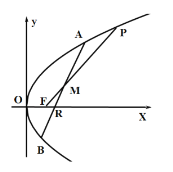
(1)若直线![]() 的斜率为1,求点
的斜率为1,求点![]() 的坐标;
的坐标;
(2)若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲和乙两个人计划周末参加志愿者活动,约定在周日早上8:00至8:30之间到某公交站搭乘公交车一起去,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
班公交车到达该站,到站的时间分别为8:05,8:15,8:30,如果他们约定见车就搭乘,则甲和乙两个人恰好能搭乘同一班公交车去的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com