分析:(1)利用新定义,代入计算,可得{bn}的通项公式.
(2)表示出数列{cn}的“生成数列”{ln}的通项,分类讨论,可得结论;
(3)表示出Ln,再分类讨论,即可求数列{Ln}的前n项和Tn.
解答:解:(1)∵a
n=n,
b1=a1 ,bn=an+an-1 (n≥2,n∈N*)∴
bn=∴b
n=2n-1;
(2)
ln= | | A+B n=1 | | 2An+2B-A n≥2 ,n∈N* |
| |
当B=0时,l
n=2An-A,由于l
n+1-l
n=2A(常数),所以此时数列{c
n}的“生成数列”{l
n}是等差数列.
当B≠0时,由于l
1=A+B,l
2=3A+2B,l
3=5A+2B,此时l
1+l
3≠2l
2,
所以此时数列{c
n}的“生成数列”{l
n}不是等差数列.
(3)
pn=,
Ln= | | 2n+n n是奇数 | | 3•2n-1+2n-1 n是偶数 |
| |
当n是偶数时,
Tn=(2+1)+(23+3)+(25+5)+…+(2n-1+(n-1))+(3•2+3)+(3•23+7)+…+(3•2n-1+(2n-1))=
(2n-1)++2n+1-2+=
(2n-1)+当n是奇数时,T
n=T
n+1-p
n+1=
(2n+1-1)+-(3•2n+(2n+1))=
+-=+n2-综合:
Tn=.
点评:本题考查新定义,考查数列的求和,考查学生分析解决问题的能力,属于中档题.



 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图. 已知数列{an}满足如图所示的流程图
已知数列{an}满足如图所示的流程图 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图.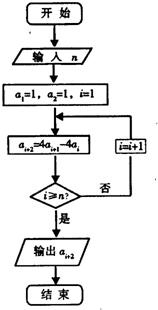 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图. 是等差数列,并求{an}的通项公式.
是等差数列,并求{an}的通项公式.