
(Ⅰ)设点P分有向线段![]() 所成的比为λ,证明:
所成的比为λ,证明: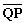 ⊥(
⊥(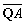 -λ
-λ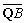 );
);
(Ⅱ)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
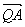
21.解:
(Ⅰ)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程x2=4y得x2-4kx-4m=0. ①
设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根.
所以x1x2=-4m.
由点P(0,m)分有向线段![]() 所成的比为λ,得
所成的比为λ,得![]() =0,即λ=-
=0,即λ=-![]() .
.
又点Q是点P关于原点的对称点,
故点Q的坐标是(0,-m),从而![]() =(0,2m).
=(0,2m).
![]() -λ
-λ![]() =(x1,y1+m)-λ(x2,y2+m)
=(x1,y1+m)-λ(x2,y2+m)
=(x1-λx2,y1-λy2+(1-λ)m).
![]() ·(
·(![]() -λ
-λ![]() )=2m[y1-λy2+(1-λ)m]
)=2m[y1-λy2+(1-λ)m]
=2m[![]() +
+![]() ·
·![]() +(1+
+(1+![]() )m]
)m]
=2m(x1+x2)·![]()
=2m(x1+x2)·![]()
=0,
所以![]() ⊥(
⊥(![]() -λ
-λ![]() ).
).
(Ⅱ)由![]() 得点A、B的坐标分别是(6,9)、(-4,4).
得点A、B的坐标分别是(6,9)、(-4,4).
由x2=4y得y=![]() x2,y′=
x2,y′=![]() x,
x,
所以抛物线x2=4y在点A处切线的斜率为y′|x=6=3.
设圆C的方程是(x-a)2+(y-b)2=r2,
由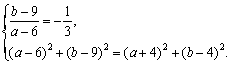
解之得a=-![]() ,b=
,b=![]() ,r2=(a+4)2+(b-4)2=
,r2=(a+4)2+(b-4)2=![]() .
.
所以圆C的方程是(x+![]() )2+(y-
)2+(y-![]() )2=
)2=![]() ,
,
即x2+y2+3x-23y+72=0.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.| AB |
| QP |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.| AP |
| PB |
| x1 |
| x2 |
| QP |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
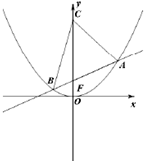 (2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
(2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).| 9 |
| 2 |
| 64 |
| 7 |
查看答案和解析>>
科目:高中数学 来源:2004年湖南省高考数学试卷(文科)(解析版) 题型:解答题
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点. 所成的比为λ,证明:
所成的比为λ,证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com