
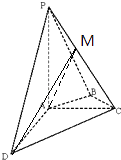
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(1)证明PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值.
【答案】
(1)证明:∵PA⊥平面ABCD,DA平面ABCD,
∴DA⊥PA,
又∵AC⊥AD,PA∩AC=A,
∴DA⊥面PAC,
又PC面PAC,∴DA⊥PC
(2)证明:过A作AM⊥PC交PC于M,连接DM,则∠AMD为所求角,
在Rt△PAC中,AM= ![]() ,
,
在Rt△DAM中,DM= ![]() ,
,
在Rt△AMD中,sin∠AMD= ![]() .
.
∴二面角A﹣PC﹣D的正弦值为 ![]() .
.
【解析】(1)推导出DA⊥PA,AC⊥AD,从而DA⊥面PAC,由此能证明DA⊥PC.(2)过A作AM⊥PC交PC于M,连接DM,则∠AMD为所求角,由此能求出二面角A﹣PC﹣D的正弦值.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x﹣1)的图象关于直线x=1对称,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0成立若a=(20.2)f(20.2),b=(1n2)f(1n2),c=( ![]() )f(
)f( ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:点
,证明:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“已知函数y=f(x),x∈ D,若D关于原点对称,则函数y=f(x),x∈ D为奇函数”的逆命题;
②“对应边平行的两角相等”的否命题;
③“若a≠0,则方程ax+b=0有实根”的逆否命题;
④“若A∪ B=B,则B≠A”的逆否命题.
其中的真命题是( )
A. ①② B. ②③
C. ①③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=10n﹣n2(n∈N*),又bn=|an|(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com