练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．函数f（x）=3x2-lnx-x的极值点的个数是（　　）
    A．0B．1C．2D．3

    分析 可看出f（x）定义域为（0，+∞），然后求导数$f′（x）=\frac{（2x-1）（3x+1）}{x}$，从而根据二次函数的图象即可判断导数符号，进而可得出f（x）的极值点，即得出极值点的个数．

    解答 解：函数f（x）的定义域为（0，+∞）；
    $f′（x）=6x-\frac{1}{x}-1=\frac{6{x}^{2}-x-1}{x}$=$\frac{（2x-1）（3x+1）}{x}$；
    ∴$0＜x＜\frac{1}{2}$时，f′（x）＜0，$x＞\frac{1}{2}$时，f′（x）＞0；
    ∴$x=\frac{1}{2}$是f（x）的极值点；
    即f（x）的极值点个数为1．
    故选B．

    点评 考查对数函数的定义域，根据导数求函数极值点的方法和过程，熟悉二次函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+4x-3，1≤x≤3}\\{x-3，x＞3}\\{\;}\end{array}\right.$，若在其定义域内存在n（n≥2，n∈N*）个不同的数x1，x2，…，xn，使得$\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$=…=$\frac{f（{x}_{n}）}{{x}_{n}}$，则n的最大值是3；若n=2，则$\frac{f（{x}_{n}）}{{x}_{n}}$的最大值等于4-$2\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数f（x）=$\left\{\begin{array}{l}|{lnx}|，（{0＜x≤{e^2}}）\\{e^2}+2-x，（{x＞{e^2}}）\end{array}$，存在x1＜x2＜x3，f（x1）=f（x2）=f（x3），则$\frac{{f（{x_3}）}}{{{x_1}{x_2}^2}}$的最大值为（　　）
    A．$\frac{1}{{2\sqrt{e}}}$B．$\frac{1}{{\sqrt{e}}}$C．$\frac{1}{e}$D．$\frac{1}{e^2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=xlnx，g（x）═ax2-（a+1）x+1（a∈R），当a=0时，求f（x）+g（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知点A（$\frac{{\sqrt{3}}}{2}$，$\frac{1}{2}$），将OA绕坐标原点O逆时针旋转$\frac{π}{2}$至OB，则点B的坐标为（　　）
    A．（-$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}$）B．（$\frac{1}{2}$，-$\frac{{\sqrt{3}}}{2}$）C．（-$\frac{{\sqrt{3}}}{2}$，$\frac{1}{2}$）D．（$\frac{{\sqrt{3}}}{2}$，-$\frac{1}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≤2}\\{x+y≥0}\\{x≤4}\end{array}\right.$，则z=3x-y的最大值为（　　）
    A．-6B．10C．12D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\sqrt{3}$sinxcosx-sin2x+$\frac{1}{2}$．
    （1）求f（x）的最小正周期值；
    （2）求f（x）的单调递增区间；
    （3）求f（x）在[0，$\frac{π}{2}$]上的最值及取最值时x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．阅读如图所示的程序框图，若输入n=2017，则输出的S值是（　　）
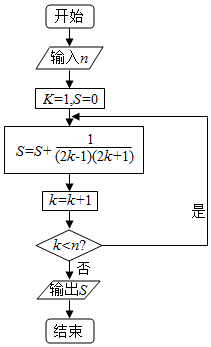
    A．$\frac{2016}{4033}$B．$\frac{2017}{4035}$C．$\frac{4032}{4033}$D．$\frac{4034}{4035}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知圆C1：x2+y2=4与x轴左右交点分别为A1、A2，过点A1的直线l1与过点A2的直线l2相交于点D，且l1与l2斜率的乘积为-$\frac{1}{4}$．
    （Ⅰ）求点D的轨迹C2方程；
    （Ⅱ）若直线l：y=kx+m不过A1、A2且与轨迹C2仅有一个公共点，且直线l与圆C1交于P、Q两点．求△POA1与△QOA2的面积之和的最大值．

    查看答案和解析>>

    同步练习册答案