
分析 设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{BA}$=$\overrightarrow{a}-\overrightarrow{b}$.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|,可得△OAB是等边三角形.设$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{AC}$=$\overrightarrow{c}-\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{c}-\overrightarrow{b}$.由<$\overrightarrow{c}-\overrightarrow{a},\overrightarrow{c}-\overrightarrow{b}$>=$\frac{2π}{3}$,可得点C在△ABC的外接圆上,则当OC为△ABC的外接圆的直径时,$\frac{|\overrightarrow{c}|}{|\overrightarrow{a}|}$取得最大值.
解答 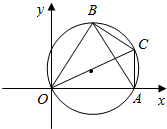 解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{BA}$=$\overrightarrow{a}-\overrightarrow{b}$.
解:设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{BA}$=$\overrightarrow{a}-\overrightarrow{b}$.
∵非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|,
∴△OAB是等边三角形.
设$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{AC}$=$\overrightarrow{c}-\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{c}-\overrightarrow{b}$.
∵<$\overrightarrow{c}-\overrightarrow{a},\overrightarrow{c}-\overrightarrow{b}$>=$\frac{2π}{3}$,
∴点C在△ABC的外接圆上,
则当OC为△ABC的外接圆的直径时,$\frac{|\overrightarrow{c}|}{|\overrightarrow{a}|}$取得最大值=$\frac{1}{cos3{0}^{°}}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了向量的三角形法则、等边三角形的性质、三角形外接圆的性质、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 80 | C. | 100 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com