
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
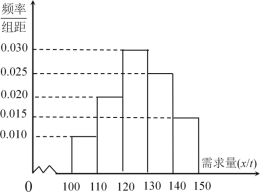
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
【答案】(1)![]() ;(2)0.7;(3)平均数为
;(2)0.7;(3)平均数为![]() (吨),估计中位数应为
(吨),估计中位数应为![]() (吨)
(吨)
【解析】
(1)分别计算![]() 和
和![]() 时T的值,用分段函数表示T的解析式;
时T的值,用分段函数表示T的解析式;
(2)计算利润T不少于57万元时x的取值范围,求出对应的频率值即可;
(3)利用每一小组底边的中点乘以对应的矩形的面积(即频率)求和得出平均数,根据中位数两边频率相等(即矩形面积和相等)求出中位数的大小.
解:(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以,![]() ;
;
(2)根据频率分布直方图及(1)知,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,由
时,由![]()
所以,利润![]() 不少于57万元当且仅当
不少于57万元当且仅当![]() ,
,
于是由频率分布直方图可知市场需求量![]() 的频率为
的频率为
![]() ,
,
所以下一个销售季度内的利润![]() 不少于57万元的概率的估计值为0.7;
不少于57万元的概率的估计值为0.7;
(3)估计一个销售季度内市场需求量![]() 的平均数为
的平均数为
![]()
![]() (吨)
(吨)
由频率分布直方图易知,
由于![]() 时,对应的频率为
时,对应的频率为![]() ,
,
而![]() 时,对应的频率为
时,对应的频率为![]() ,
,
因此一个销售季度内市场需求量![]() 的中位数应属于区间
的中位数应属于区间![]() ,于是估计中位数应为
,于是估计中位数应为![]() (吨).
(吨).


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】对某产品1到6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与单价仍然服从(1)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校书店新进了一套精品古典四大名著:《红楼梦》、《三国演义》、《西游记》、《水浒传》共四本书,每本名著数量足够多,今有五名同学去书店买书,由于价格较高,五名同学打算每人只选择一本购买.
(1)求“每本书都有同学买到”的概率;
(2)求“对于每个同学,均存在另一个同学与其购买的书相同”的概率;
(3)记X为五位同学购买相同书的个数的最大值,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
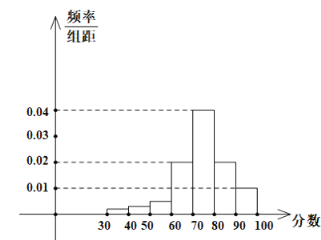
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为x=﹣2,且直线l与x轴交于点M,圆O:![]() 与x轴交于A,B两点(如图).
与x轴交于A,B两点(如图).
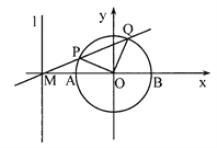
(1)过M点的直线l1交圆于P、Q两点,且O点到直线l1的距离为![]() ,求直线l1的方程;
,求直线l1的方程;
(2)求以l为准线,中心在原点,且短轴长为圆O的半径的椭圆方程;
(3)过M点的圆的切线l2,交(2)中的一个椭圆于C、D两点,其中C、D两点在x轴上方,求线段CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)﹣f(x1)](x2﹣x1)<0恒成立,设a=f(![]() ),b=f(2),c=f(3),则a、b、c的大小关系为( )
),b=f(2),c=f(3),则a、b、c的大小关系为( )
A.c>a>bB.c>b>aC.a>c>bD.b>a>c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数,![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图像过点
的图像过点![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)若![]() ,试判断函数
,试判断函数![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)设函数 ,若对每一个不小于3的实数
,若对每一个不小于3的实数![]() ,都恰有一个小于3的实数
,都恰有一个小于3的实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(1)求a的值,并写出函数f(x)的单调区间(不需要求解过程);
(2)若关于x的方程![]() 在[2,3]上有解,求k的取值范围.
在[2,3]上有解,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com