
【题目】2019年“非洲猪瘟”过后,全国生猪价格逐步上涨,某大型养猪企业,欲将达到养殖周期的生猪全部出售,根据去年的销售记录,得到销售生猪的重量的频率分布直方图(如图所示).

(1)根据去年生猪重量的频率分布直方图,估计今年生猪出栏(达到养殖周期)时,生猪重量达不到270斤的概率(以频率代替概率);
(2)若假设该企业今年达到养殖周期的生猪出栏量为5000头,生猪市场价格是30元/斤,试估计该企业本养殖周期的销售收入是多少万元;
(3)若从本养殖周期的生猪中,任意选两头生猪,其重量达到270斤及以上的生猪数为随机变量![]() ,试求随机变量
,试求随机变量![]() 的分布列及方差.
的分布列及方差.
【答案】(1)![]() (2)
(2)![]() (万元)(3)详见解析
(万元)(3)详见解析
【解析】
(1)根据生猪重量的频率分布直方图,即可求得生猪重量达不到270斤的概率.
(2)根据频率分布直方图,先求得生猪重量的平均值,即可由总量及单价求得该企业本养殖周期的销售收入.
(3)由(1)可得重量达到270斤及以上的概率. 由题意可得随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,结合二项分布即可求得各自的概率,进而得分布列;再由方差公式即可得解.
,结合二项分布即可求得各自的概率,进而得分布列;再由方差公式即可得解.
(1)估计生猪重量达不到270斤的概率为
![]() .
.
(2)生猪重量的平均数为![]()
![]()
![]()
![]() (斤).
(斤).
所以估计该企业本养殖周期的销售收入是![]()
![]() (万元).
(万元).
(3)由(1)可得随机选一头生猪,其重量达到270斤及以上的概率为![]() ,
,
由题意可得随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴随机变量![]() 的分布列为
的分布列为
Y | 0 | 1 | 2 |
P |
|
|
|
∴随机变量![]() 的方差
的方差![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,圆
,圆![]() :
:![]() 过椭圆
过椭圆![]() 的三个顶点,过点
的三个顶点,过点![]() 的直线
的直线![]() (斜率存在且不为0)与椭圆
(斜率存在且不为0)与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)证明:在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值,并求出定点
为定值,并求出定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】日本数学家角谷静夫发现的“![]() 猜想”是指:任取一个自然数,如果它是偶数,我们就把它除以
猜想”是指:任取一个自然数,如果它是偶数,我们就把它除以![]() ,如果它是奇数我们就把它乘
,如果它是奇数我们就把它乘![]() 再加上
再加上![]() ,在这样一个变换下,我们就得到了一个新的自然数。如果反复使用这个变换,我们就会得到一串自然数,猜想就是:反复进行上述运算后,最后结果为
,在这样一个变换下,我们就得到了一个新的自然数。如果反复使用这个变换,我们就会得到一串自然数,猜想就是:反复进行上述运算后,最后结果为![]() ,现根据此猜想设计一个程序框图如图所示,执行该程序框图输入的
,现根据此猜想设计一个程序框图如图所示,执行该程序框图输入的![]() ,则输出
,则输出![]() 值为( )
值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的个数是( )
①直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
②![]() 为异面直线,则过
为异面直线,则过![]() 且与
且与![]() 平行的平面有且仅有一个;
平行的平面有且仅有一个;
③直四棱柱是直平行六面体;
④两相邻侧面所成角相等的棱锥是正棱锥.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车尾气中含有一氧化碳(![]() ),碳氢化合物(
),碳氢化合物(![]() )等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
)等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
不了解 | 了解 | 总计 | |
女性 |
|
| 50 |
男性 | 15 | 35 | 50 |
总计 |
|
| 100 |
(1)若从这100人中任选1人,选到了解机动车强制报废标准的人的概率为![]() ,问是否有
,问是否有![]() 的把握认为“对机动车强制报废标准是否了解与性别有关”?
的把握认为“对机动车强制报废标准是否了解与性别有关”?
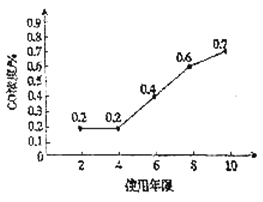
(2)该环保组织从相关部门获得某型号汽车的使用年限与排放的尾气中![]() 浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中
浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中![]() 浓度
浓度![]() 与使用年限
与使用年限![]() 线性相关,试确定
线性相关,试确定![]() 关于
关于![]() 的回归方程,并预测该型号的汽车使用12年排放尾气中的
的回归方程,并预测该型号的汽车使用12年排放尾气中的![]() 浓度是使用4年的多少倍.
浓度是使用4年的多少倍.
附: (
(![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:用最小二乘法求线性回归方程系数公式: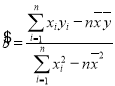 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com