
 ,向量
,向量 与向量
与向量 夹角为
夹角为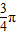 ,且
,且 ,又A、B、C为△ABC的三个内角,且B=
,又A、B、C为△ABC的三个内角,且B= ,A≤B≤C.
,A≤B≤C. ;
; 与向量
与向量 的夹角为
的夹角为 ,向量
,向量 ,试求
,试求 的取值范围.
的取值范围.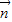 =(x,y),由
=(x,y),由 可得x+y=-1,由向量
可得x+y=-1,由向量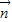 与向量
与向量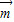 夹角为
夹角为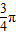 ,求得x2+y2=1,解方程组求得x、y的值,即可求得向量
,求得x2+y2=1,解方程组求得x、y的值,即可求得向量 的坐标.
的坐标.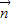 与向量
与向量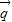 =(1,0)垂直知
=(1,0)垂直知 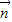 =(0,-1),求得
=(0,-1),求得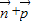 的坐标,可求得
的坐标,可求得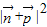 的解析式为
的解析式为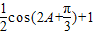 ,再根据余弦函数的定义域和值域,求得
,再根据余弦函数的定义域和值域,求得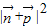 的范围,即可得到
的范围,即可得到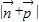 的取值范围.
的取值范围.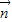 =(x,y),由
=(x,y),由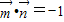 可得x+y=-1. ①…(2分)
可得x+y=-1. ①…(2分)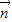 与向量
与向量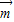 夹角为
夹角为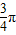 ,得
,得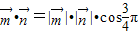 ,∴
,∴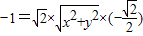 ,得x2+y2=1.②…(4分)
,得x2+y2=1.②…(4分)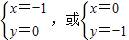 ,可得
,可得 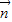 =(-1,0),或
=(-1,0),或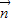 =(0,-1). …(6分)
=(0,-1). …(6分)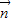 与向量
与向量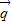 =(1,0)垂直知
=(1,0)垂直知 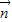 =(0,-1). …(7分)
=(0,-1). …(7分)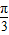 ,A≤B≤C,∴
,A≤B≤C,∴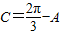 ,
,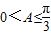 . …(8分)
. …(8分)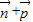 =(cosA,
=(cosA, -1)=(cosA,cosC),…(9分)
-1)=(cosA,cosC),…(9分)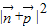 =cos2A+cos2C=
=cos2A+cos2C= …(10分)
…(10分)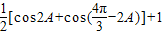 =
=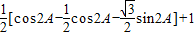 =
=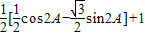 =
=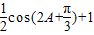 . …(12分)
. …(12分)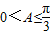 ,∴
,∴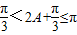 ,∴
,∴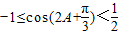 ,∴
,∴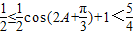 .
.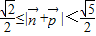 ,即
,即 的取值范围是
的取值范围是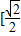 ,
,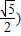 . …(14分)
. …(14分)

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2010-2011学年浙江省杭州市学军中学高三(上)期中数学试卷(文科)(解析版) 题型:解答题
 =
= ,向量
,向量 与向量
与向量 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间;查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州市萧山九中高三数学暑假作业3(文科)(解析版) 题型:解答题
 =
= ,向量
,向量 与向量
与向量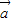 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间;查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省嘉兴市桐乡一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
 =
= ,向量
,向量 与向量
与向量 关于x轴对称.
关于x轴对称. 的解析式,并求其单调增区间;
的解析式,并求其单调增区间;查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省高一下学期第一次月考数学试卷 题型:解答题
已知向量 ,向量
,向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 ;
;
(1)求向量 ;
;
(2)设向量 ,向量
,向量 ,其中
,其中 ,若
,若 ,求
,求 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com