Question

【题目】设集合A={x|0≤x≤2}，B={y|1≤y≤2}，若对于函数y=f（x），其定义域为A，值域为B，则这个函数的图象可能是（ ）
A.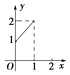
B.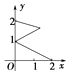
C.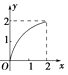
D.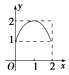

Answer 1

【答案】D
【解析】解：由函数定义知A定义域为[0，1]，故A不满足题意；
B表示函数的图象值域为[0，2]，故B不满足题意；
C函数的值域为[0，2]，故C不满足题意；
D的定义域与值域都与题目相符，故D满足题意．

所以答案是：D．

【考点精析】通过灵活运用函数的图象和函数的定义域及其求法，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值；求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零即可以解答此题．