
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是
是![]() 上一点,且线段
上一点,且线段![]() 的中点坐标为
的中点坐标为![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,
,![]() 为抛物线
为抛物线![]() 上的两个动点(异于点
上的两个动点(异于点![]() ),且
),且![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,
,![]() 分别为椭圆C的左、右焦点且
分别为椭圆C的左、右焦点且![]() .
.

(1)求椭圆C的方程;
(2)过P点的直线![]() 与椭圆C有且只有一个公共点,直线
与椭圆C有且只有一个公共点,直线![]() 平行于OP(O为原点),且与椭圆C交于两点A、B,与直线
平行于OP(O为原点),且与椭圆C交于两点A、B,与直线![]() 交于点M(M介于A、B两点之间).
交于点M(M介于A、B两点之间).
(i)当![]() 面积最大时,求
面积最大时,求![]() 的方程;
的方程;
(ii)求证:![]() ,并判断
,并判断![]() ,
,![]() 的斜率是否可以按某种顺序构成等比数列.
的斜率是否可以按某种顺序构成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为1,E,F分别是
的边长为1,E,F分别是![]() ,
,![]() 的中点,
的中点,![]() 交EF于点D,现沿SE,SF及EF把这个正方形折成一个四面体,使
交EF于点D,现沿SE,SF及EF把这个正方形折成一个四面体,使![]() ,
,![]() ,
,![]() 三点重合,重合后的点记为G,则在四面体
三点重合,重合后的点记为G,则在四面体![]() 中必有( )
中必有( )

A.![]() 平面EFG
平面EFG
B.设线段SF的中点为H,则![]() 平面SGE
平面SGE
C.四面体![]() 的体积为
的体积为![]()
D.四面体![]() 的外接球的表面积为
的外接球的表面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 且
且![]() ,点
,点![]() 在椭圆内部,点
在椭圆内部,点![]() 在椭圆上,则以下说法正确的是( )
在椭圆上,则以下说法正确的是( )
A.![]() 的最小值为
的最小值为![]()
B.椭圆![]() 的短轴长可能为2
的短轴长可能为2
C.椭圆![]() 的离心率的取值范围为
的离心率的取值范围为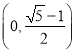
D.若![]() ,则椭圆
,则椭圆![]() 的长轴长为
的长轴长为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为彻底打赢脱贫攻坚战,2020年春,某市政府投入资金帮扶某农户种植蔬菜大棚脱贫致富,若该农户计划种植冬瓜和茄子,总面积不超过15亩,帮扶资金不超过4万元,冬瓜每亩产量10 000斤,成本2000元,每斤售价0.5元,茄子每亩产量5000斤,成本3000元,每斤售价1.4元,则该农户种植冬瓜和茄子利润的最大值为( )
A.4万元B.5.5万元C.6.5万元D.10万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某志愿者服务网站在线招募志愿者,当报名人数超过计划招募人数时,将采用随机抽取的方法招募志愿者,如表记录了A,B,C,D四个项目最终的招募情况,其中有两个数据模糊,记为a,b.
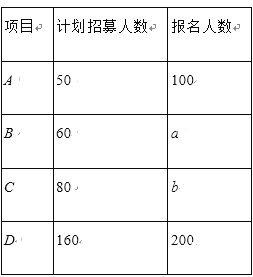
甲同学报名参加了这四个志愿者服务项目,记ξ为甲同学最终被招募的项目个数,已知P(ξ=0)![]() ,P(ξ=4)
,P(ξ=4)![]() .
.
(Ⅰ)求甲同学至多获得三个项目招募的概率;
(Ⅱ)求a,b的值;
(Ⅲ)假设有十名报了项目A的志愿者(不包含甲)调整到项目D,试判断Eξ如何变化(结论不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com