
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评.同时也为公司赢得丰厚的利润,该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关)
的统计数据如下表(已知该公司的年利润与年份代号线性相关)
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 | 29 | 33 | 36 | 44 | 48 | 52 | 59 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年的年利润;
的线性回归方程,并预测该公司2020年的年利润;
(2)当统计表中某年年利润的实际值大于由(1)中线性回归方程计算出该年利润的估计值时,称该年为A级利润年,否则称为B级利润年.现从2015年至2019年这5年中随机抽取2年,求恰有1年为A级利润年的概率.
参考公式: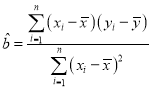 ,
,![]()
【答案】(1)![]() ,63亿元.(2)
,63亿元.(2)![]()
【解析】
(1)利用回归直线方程计算公式,计算出回归直线方程,并作出预测.
(2)利用列举法,结合古典概型概率计算公式,计算出所求概率.
(1)因为![]() ,
,
![]() ,
,
所以 ,所以
,所以![]() ,
,
所以回归直线方程为![]() .
.
所以当![]() 时,
时,![]() ,
,
即预测该公司2020年的年利润为63亿元.
(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以从2015—2019年有2年A级利润年记为a,b,
,所以从2015—2019年有2年A级利润年记为a,b,
有3年B级利润年记为1,2,3,
所以基本事件有:
(a,b)(a,1)(a,2),(a,3),(b,1),(b,2),(b,3),(1,2),(1,3),(2,3)共10个
令“恰有1年为A级利润年”为事件M,事件M包含的基本事件有6个,
所以![]() ,
,


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】某电视台为宣传本市,随机对本市内![]() 岁的人群抽取了
岁的人群抽取了![]() 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |

(1)分别求出![]() 的值;
的值;
(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(1≤x≤30,x∈N+)天的销售价格(单位:元/件)为f(x)=![]() 第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
第x天的销售量(单位:件)为g(x)=a-x(a为常数),且在第20天该商品的销售收入为1 200元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.
两点.
(1)若以![]() 为直径的动圆内切于圆
为直径的动圆内切于圆![]() ,求椭圆的长轴长;
,求椭圆的长轴长;
(2)当![]() 时,问在
时,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?并说明理由.
为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() .记
.记![]() .给出下列关于函数
.给出下列关于函数![]() 的说法:①当
的说法:①当![]() 时,
时,![]() ;②函数
;②函数![]() 为奇函数;③函数
为奇函数;③函数![]() 在
在![]() 上为增函数;④函数
上为增函数;④函数![]() 的最小值为
的最小值为![]() ,无最大值.其中正确的是______.
,无最大值.其中正确的是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·牡丹江一中]某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数和平均数分别是( )

A. 73.3,75,72 B. 73.3,80,73
C. 70,70,76 D. 70,75,75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() (
(![]() )的直线
)的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com