
【题目】如图,在直二面角![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 是以
是以![]() 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() .
.
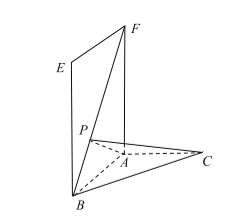
(Ⅰ)证明:![]() 面
面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)要证线面垂直,一般要证两个线线垂直,观察直角三角形![]() 中,由已知三个线段长,可由射影定理(或相似三角形)由平面几何知识可证
中,由已知三个线段长,可由射影定理(或相似三角形)由平面几何知识可证![]() (也可余弦定理求出
(也可余弦定理求出![]() ,再勾股定理证得此结论.),另外有面面垂直,用
,再勾股定理证得此结论.),另外有面面垂直,用![]() ,可得
,可得![]() 与平面
与平面![]() 垂直,从而有
垂直,从而有![]() ,有了这两个线线垂直,就可得线面垂直;(Ⅱ)要求二面角,图形中
,有了这两个线线垂直,就可得线面垂直;(Ⅱ)要求二面角,图形中![]() 两两垂直,以它们坐标轴建立空间直角坐标系后,可写出各点坐标,从而可求得平面
两两垂直,以它们坐标轴建立空间直角坐标系后,可写出各点坐标,从而可求得平面![]() 和平面
和平面![]() 的法向量,由法向量夹角与二面角相等(或互补)可求得二面角.
的法向量,由法向量夹角与二面角相等(或互补)可求得二面角.
试题解析:(Ⅰ)证明:由题意知:![]() ,
,![]() ,
,
![]() .
.
∵![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)知![]() 、
、![]() 、
、![]() 两两互相垂直,以
两两互相垂直,以![]() 为原点,
为原点,![]() 方向为
方向为![]() 轴的正方向建立如图所示空间直角坐标系,则
轴的正方向建立如图所示空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则 ,
,
∴ ,取
,取![]() 得平面
得平面![]() 的一个法向量
的一个法向量![]() ,
,
又平面![]() 的一个法向量
的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,由题中条件可知
,由题中条件可知![]() ,
,
则 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.



 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】根据下面对几何体结构特征的描述,说出几何体的名称.
(1)由8个面围成,其中2个面是互相平行且全等的六边形,其他各面都是平行四边形.
(2)由5个面围成,其中一个是正方形,其他各面都是有1个公共顶点的三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中,正确的是( )
A.四边形是平面图形
B.有三个公共点的两个平面重合。
C.两两相交的三条直线必在同一个平面内
D.三角形必是平面图形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12 m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a m,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3 m,且不计房屋背面的费用.当侧面的长度为多少时,总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从学号为0~50的高一某班50名学生中随机选取5名同学参加数学测试,采用系
统抽样的方法,则所选5名学生的学号可能是:( )
A、5,15,25,35,45 B、1,2,3,4,5
C、2,4,6,8,10 D、 4,13,22,31,40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:

(1)根据上表数据结合散点图,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系并说明理由:①
的变化关系并说明理由:①![]() ;②
;②![]() ;③
;③![]() .
.
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:x>0,x-lnx>0,则¬p为
A. x0>0,x0-lnx0>0 B. x0>0,x0-lnx0≤0
C. x>0,x-lnx<0 D. x>0,x-lnx≤0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com