
分析 (1)由${S_n}={n^2}+2n,n∈{N^*}$,当n=1时,a1=S1=3.当n≥2时,an=Sn-Sn-1,即可得出.
(2)由(1)可得,${b_n}=(2n+1)•{3^n}$.再利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵${S_n}={n^2}+2n,n∈{N^*}$,
∴当n=1时,a1=S1=3.
$当n≥2时,{a_n}={S_n}-{S_{n-1}}=({n^2}+2n)-[{(n-1)^2}+2(n-1)]=2n+1$(*),
显然,当n=1时也满足(*)式,
综上所述,${a_n}=2n+1,(n∈{N^*})$.
(2)由(1)可得,${b_n}=(2n+1)•{3^n}$.
其前n项和${{T}_n}=3×3+5×{3^2}+7×{3^3}+…+(2n+1)•{3^n}$①
则 $3{{T}_n}=3×{3^2}+5×{3^3}+7×{3^4}+…+(2n+1)•{3^{n+1}}$②
①-②得,$-2{{T}_n}=9+2({3^2}+{3^3}+{3^4}+…+{3^n})-(2n+1)•{3^{n+1}}$
=$9+2×\frac{{9(1-{3^{n-1}})}}{1-3}-(2n+1)•{3^{n+1}}$
=-2n•3n+1,
∴${T_n}=n•{3^{n+1}}$.
点评 本题考查了递推关系、“错位相减法”与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相等 | B. | 仅是模相等 | C. | 不相等 | D. | 共线但不相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ②④⑤ | C. | ①③⑤ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
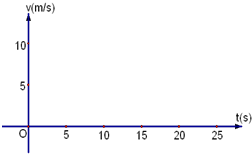 一小车A从静止开始以2m/s2的加速度作匀加速度直线运动,持续5秒钟后作加速度为0的匀速直线运动,并保持10秒,最后以-1m/s2的加速度作匀减速度直线运动直至小车静止.另有一小车B在同一起点,从开始时刻以速度v0作匀速直线运动.
一小车A从静止开始以2m/s2的加速度作匀加速度直线运动,持续5秒钟后作加速度为0的匀速直线运动,并保持10秒,最后以-1m/s2的加速度作匀减速度直线运动直至小车静止.另有一小车B在同一起点,从开始时刻以速度v0作匀速直线运动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2009 | B. | -3010 | C. | -3014 | D. | 3028 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com