
【题目】等比数列{an}的前n项和为Sn , 已知对任意的n∈N+ , 点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
(1)求r的值.
(2)当b=2时,记bn=2(log2an+1)(n∈N+),证明:对任意的n∈N+,不等式成立 ![]() .
.
【答案】
(1)解:(1)因为对任意的n∈N+,点(n,Sn),
均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
所以得Sn=bn+r,当n=1时,a1=S1=b+r,
当n≥2时,an=Sn﹣Sn﹣1=bn+r﹣(bn﹣1+r)=bn﹣bn﹣1=(b﹣1)bn﹣1,
又因为{an}为等比数列,所以r=﹣1,公比为b,an=(b﹣1)bn﹣1
(2)当b=2时,an=(b﹣1)bn﹣1=2n﹣1,bn=2(log2an+1)=2(log22n﹣1+1)=2n
则 ![]() ,
,
所以 ![]()
下面用数学归纳法证明不等式 ![]()
![]() 成立.
成立.
当n=1时,左边= ![]() ,右边=
,右边= ![]() ,
,
因为 ![]() ,所以不等式成立.
,所以不等式成立.
假设当n=k时不等式成立,
即 ![]()
![]() 成立
成立
则当n=k+1时,
左边= ![]()

所以当n=k+1时,不等式也成立.
由①、②可得不等式恒成立
【解析】本题考查的数学归纳法及数列的性质.(1)由已知中因为对任意的n∈N+ , 点(n,Sn),均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.根据数列中an与Sn的关系,我们易得到一个关于r的方程,再由数列{an}为等比数列,即可得到r的值.(2)将b=2代入,我们可以得到数列{an}的通项公式,再由bn=2(log2an+1)(n∈n),我们可给数列{bn}的通项公式,进而可将不等式 ![]() 进行简化,然后利用数学归纳法对其进行证明.
进行简化,然后利用数学归纳法对其进行证明.
【考点精析】根据题目的已知条件,利用数学归纳法的定义的相关知识可以得到问题的答案,需要掌握数学归纳法是证明关于正整数n的命题的一种方法.


科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC 
(1)证明:A1C⊥平面BED;
(2)求二面角A1﹣DE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,D是AC的中点,EF∥DB. 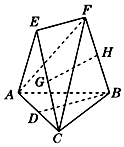
(1)已知AB=BC,AF=CF,求证:AC⊥平面BEF;
(2)已知G、H分别是EC和FB的中点,求证:GH∥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列结论的证法,再解决后面的问题:已知a1 , a2∈R,a1+a2=1,求证a12+a22≥ ![]() .
.
【证明】构造函数f(x)=(x﹣a1)2+(x﹣a2)2
则f(x)=2x2﹣2(a1+a2)x+a12+a22
=2x2﹣2x+a12+a22
因为对一切x∈R,恒有f(x)≥0.
所以△=4﹣8(a12+a22)≤0,从而得a12+a22≥ ![]() ,
,
(1)若a1 , a2 , …,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设AB=PC=2,BC=1,求三棱锥P-BEF的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 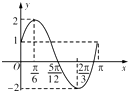
(1)求函数的解析式;
(2)设 ![]() π<x<
π<x< ![]() π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com