
【题目】已知![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)增区间为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)求出![]() ,令
,令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)不等式
的减区间;(Ⅱ)不等式![]() 恒成立,等价于当
恒成立,等价于当![]() 时,
时, 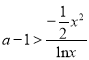 恒成立,只需
恒成立,只需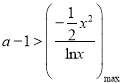 ,利用导数研究函数的单调性,求出
,利用导数研究函数的单调性,求出![]() 的最大值为
的最大值为![]() ,所以
,所以![]() ,
, ![]() .
.
试题解析:(Ⅰ) 依题意![]() ,
,
若![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,又
,又![]() ,
,
解得![]() ,所以函数
,所以函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(Ⅱ)依题意得![]() 即
即![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴ ![]() ,∴
,∴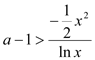 ,
,
∴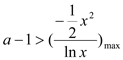 .
.
设![]()
![]() ,
, 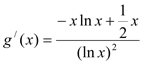 ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减;
单调递减;
∴![]() =
=![]() ,
,
∴![]() 即
即![]() .
.
【方法点晴】本题主要考查利用导数研究函数的单调性及求函数的最值、不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立
恒成立![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题(2)是利用方法 ① 求得
恒成立;④ 讨论参数.本题(2)是利用方法 ① 求得![]() 的取值范围.
的取值范围.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]() ,当直线
,当直线![]() 的倾斜角发生变化时,直线
的倾斜角发生变化时,直线![]() 与
与![]() 轴是否相交于定点?若是,求出定点坐标,否则,说明理由.
轴是否相交于定点?若是,求出定点坐标,否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
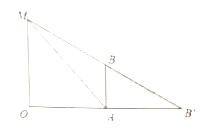
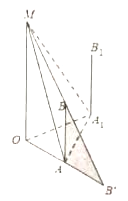
【题目】已知小明(如图中![]() 所示)身高
所示)身高![]() 米,路灯
米,路灯![]() 高
高![]() 米,
米, ![]() ,
, ![]() 均垂直于水平地面,分别与地面交于点
均垂直于水平地面,分别与地面交于点![]() ,
, ![]() .点光源从
.点光源从![]() 发出,小明在地上的影子记作
发出,小明在地上的影子记作![]() .
.
(1)小明沿着圆心为![]() ,半径为
,半径为![]() 米的圆周在地面上走一圈,求
米的圆周在地面上走一圈,求![]() 扫过的图形面积;
扫过的图形面积;
(2)若![]() 米,小明从
米,小明从![]() 出发,以
出发,以![]() 米/秒的速度沿线段
米/秒的速度沿线段![]() 走到
走到![]() ,
, ![]() ,且
,且![]() 米.
米. ![]() 秒时,小明在地面上的影子长度记为
秒时,小明在地面上的影子长度记为![]() (单位:米),求
(单位:米),求![]() 的表达式与最小值.
的表达式与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程
的极坐标方程![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,且在两坐标系中取相同的长度单位,直线
轴非负半轴建立平面直角坐标系,且在两坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为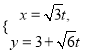 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上任意一点
上任意一点![]() 作与直线
作与直线![]() 相交的直线,该直线与直线
相交的直线,该直线与直线![]() 所成的锐角为
所成的锐角为![]() ,设交点为
,设交点为![]() ,求
,求![]() 的最大值和最小值,并求出取得最大值和最小值时点
的最大值和最小值,并求出取得最大值和最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,圆
,圆![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 不同两点.
不同两点.
(Ⅰ)求直线![]() 的斜率
的斜率![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在过点![]() 且垂直平分弦
且垂直平分弦![]() 的直线
的直线![]() ?若存在,求直线
?若存在,求直线![]() 斜率
斜率![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com