����֤����������֪��t-1��S
1=2ta
1-t-1�����a
1=1��
�ɣ�t-1��S
n=2ta
n-t-1���ã�t-1��S
n+1=2ta
n+1-t-1��
��ʽ����ã�t-1��a
n+1=2ta
n+1-2ta
n��
��
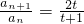
����������
������{a
n}����1���

Ϊ���ȵĵȱ����У�����4�֣�
���⣺��q=f ��t��=

��b
1=a
1=1��b
n+1=

f ��b
n��=

��
��

=

+1��
������{

}����1Ϊ���1Ϊ����ĵȲ����У�
��

������8�֣�
��III���⣺��t=

ʱ���ɣ�I��֪a
n=

����������{c
n}��1��-1��

��2��2��

��-3��-3��-3��

����
������{a
n}�ĵ�k��������{c
n}�ĵ�m
k���a
k=
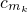
��
��k��2ʱ��m
k=k+[1+2+3+��+��k-1��]=

��
��m
9=

-45��
��S
n��ʾ����{c
n}��ǰn��ͣ���S
45=[1+

+

+��+

]+[-1+��-1��
2��2��2+��-1��
3��3��3+��+��-1��
8��8��8]��
��1+

+

+��+

=
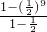
=2-
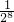
��
-1+��-1��
2��2��2+��-1��
3��3��3+��+��-1��
8��8��8=-1+2
2-3
2+4
2-5
2+6
2-7
2+8
2=��2+1����2-1��+��4+3����4-3��+��6+5����6-5��+��8+7����8-7��=3+7+11+15=36��
��S
45=2-
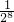
+36=38-
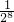
��
��S
50=S
45+��c
46+c
47+c
48+c
49+c
50��=38-
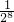
+5����-1��
9��9=-7
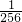
��
������{c
n}��ǰ50��֮��Ϊ-7
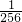
������12�֣�
�����������������е���ʽ����дһʽ����ʽ���������֤������{a
n}����1���

Ϊ���ȵĵȱ����У�
����ȷ������{

}����1Ϊ���1Ϊ����ĵȲ����У���������{

}��ͨ�ʽ��
��III��ȷ������{c
n}��1��-1��

��2��2��

��-3��-3��-3��

�������ٷ�����ͣ������������{c
n}��ǰ50��֮�ͣ�
���������⿼��ȱ�������Ȳ����е�֤�����������е�ͨ������ͣ�����ѧ���ļ��������������е��⣮

 f��bn����������{
f��bn����������{ }��ͨ�ʽ��
}��ͨ�ʽ�� ���ԣ�II���е�����{an}��������{an}��������������ak��ak+1֮�����k��
���ԣ�II���е�����{an}��������{an}��������������ak��ak+1֮�����k��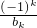 ��k��N*���õ�һ���µ����У�a1��
��k��N*���õ�һ���µ����У�a1��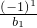 ��a2��
��a2��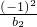 ��
��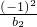 ��a3��
��a3��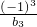 ��
��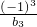 ��
��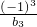 ��a4�����Ǵ�����Ϊ{cn}��������{cn}��ǰ50��֮�ͣ�
��a4�����Ǵ�����Ϊ{cn}��������{cn}��ǰ50��֮�ͣ�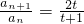 ����������
���������� Ϊ���ȵĵȱ����У�����4�֣�
Ϊ���ȵĵȱ����У�����4�֣� ��b1=a1=1��bn+1=
��b1=a1=1��bn+1= f ��bn��=
f ��bn��= ��
�� =
= +1��
+1�� }����1Ϊ���1Ϊ����ĵȲ����У�
}����1Ϊ���1Ϊ����ĵȲ����У� ������8�֣�
������8�֣� ʱ���ɣ�I��֪an=
ʱ���ɣ�I��֪an= ����������{cn}Ϊ��1��-1��
����������{cn}��1��-1�� ��2��2��
��2��2�� ��-3��-3��-3��
��-3��-3��-3�� ����
����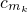 ��
�� ��
�� -45��
-45�� +
+ +��+
+��+ ]+[-1+��-1��2��2��2+��-1��3��3��3+��+��-1��8��8��8]��
]+[-1+��-1��2��2��2+��-1��3��3��3+��+��-1��8��8��8]�� +
+ +��+
+��+ =
=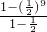 =2-
=2-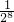 ��
��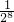 +36=38-
+36=38-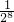 ��
��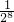 +5����-1��9��9=-7
+5����-1��9��9=-7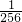 ��
�� ������12�֣�
������12�֣� Ϊ���ȵĵȱ����У�
Ϊ���ȵĵȱ����У� }����1Ϊ���1Ϊ����ĵȲ����У���������{
}����1Ϊ���1Ϊ����ĵȲ����У���������{ }��ͨ�ʽ��
}��ͨ�ʽ�� ��2��2��
��2��2�� ��-3��-3��-3��
��-3��-3��-3�� �������ٷ�����ͣ������������{cn}��ǰ50��֮�ͣ�
�������ٷ�����ͣ������������{cn}��ǰ50��֮�ͣ�

