
| NC |
| NM |
| OA |
| OB |
| NC |
| NM |
|
| OA |
| OB |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
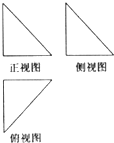 (2011•花都区模拟)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么 这个几何体的体积为( )
(2011•花都区模拟)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么 这个几何体的体积为( )查看答案和解析>>
科目:高中数学 来源: 题型:
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温 差 | 10 | 13 | 11 | 12 | 7 |
| 感染数 | 23 | 32 | 24 | 29 | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| S2 |
| b2 |
| 1 |
| Sn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com