
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() (
(![]() )上,设
)上,设![]() ,
, ![]() ,
, ![]() 分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() (
(![]() )为椭圆
)为椭圆![]() 上两点,且满足
上两点,且满足![]() ,求证:
,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
科目:高中数学 来源: 题型:
【题目】某工厂要建造一个长方体无盖贮水池,其容积为6400m3 , 深为4m,如果池底每1m2的造价为300元,池壁每1m2的造价为240元,问怎样设计水池能使总造价最低,最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
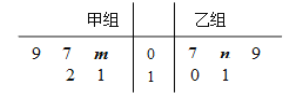
(1)分别求出![]() 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛掷一枚骰子,当它每次落地时,向上一面的点数称为该次抛掷的点数,可随机出现1到6点中的任一个结果.连续抛掷两次,第一次抛掷的点数记为a,第二次抛掷的点数记为b.
(1)求直线ax+by=0与直线x+2y+1=0平行的概率;
(2)求长度依次为a,b,2的三条线段能构成三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )在一个周期内的图像如图所示,其中M(
)在一个周期内的图像如图所示,其中M( ![]() ,2),N(
,2),N( ![]() ,0).
,0). 
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且a= ![]() ,c=3,f(
,c=3,f( ![]() )=
)= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
A.90°
B.45°
C.60°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关x的一元二次方程9x2+6ax﹣b2+4=0.
(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α,β是两个不同的平面,m,n是两条不同的直线,有如下两个命题:q:若m⊥α,n⊥β且m∥n,则α∥β;q:若m∥α,n∥β且m∥n,则α∥β.( )
A.命题q,p都正确
B.命题p正确,命题q不正确
C.命题q,p都不正确
D.命题q不正确,命题p正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为三角形ABC的三内角,其对应边分别为a,b,c,若有2acosC=2b+c成立.
(1)求A的大小;
(2)若 ![]() ,b+c=4,求三角形ABC的面积.
,b+c=4,求三角形ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com