已知函数f(x)=16ln(1+x)+x2-10x.
(1)求函数f(x)的单调区间;
(2)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
解:(1)f(x)=16ln(1+x)+x
2-10x,x∈(-1,+∞)
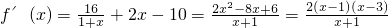
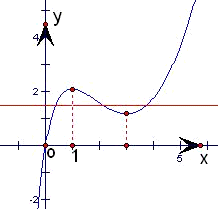
令f'(x)=0,得x=1,x=3.f'(x)和f(x)随x的变化情况如下:
| x | (-1,1) | 1 | (1,3) | 3 | (3,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
f(x)的增区间是(-1,1),(3,+∞);减区间是(1,3).
(2)由(1)知,f(x)在(-1,1)上单调递增,在(3,+∞)上单调递增,在(1,3)上单调递减.
∴f(x)
极大=f(1)=16ln2-9,f(x)
极小=f(3)=32ln2-21.
又x→-1
+时,f(x)→-∞;x→+∞时,f(x)→+∞;
可据此画出函数y=f(x)的草图(如图),由图可知,
当直线y=b与函数y=f(x)的图象有3个交点时,
当且仅当f(3)<b<f(1),
故b的取值范围为(32ln2-21,16ln2-9)
分析:(1)先根据对数函数的定义求出f(x)的定义域,并求出f′(x)=0时x的值,在定义域内,利用x的值讨论f′(x)的正负即可得到f(x)的单调区间;
(2)根据第一问函数的增减性得到函数的极大值为f(1)和极小值为f(3),然后算出x→-1
+时,f(x)→-∞;x→+∞时,f(x)→+∞;据此画出函数y=f(x)的草图,由图可知,y=b与函数f(x)的图象各有一个交点,即满足f(4)<b<f(2),即可得到b的取值范围.
点评:本题要求学生会利用导函数的正负得到函数的单调区间,会根据函数的增减性得到函数的极值,是一道综合题.

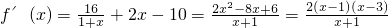
 f(x)的增区间是(-1,1),(3,+∞);减区间是(1,3).
f(x)的增区间是(-1,1),(3,+∞);减区间是(1,3).

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案