
【题目】对于双曲线![]() :
:![]() (
(![]() ),若点
),若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的外部;若点
的外部;若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的内部.
的内部.
(1)若直线![]() 上点都在
上点都在![]() 的外部,求
的外部,求![]() 的取值范围;
的取值范围;
(2)若![]() 过点
过点![]() ,圆
,圆![]() (
(![]() )在
)在![]() 内部及
内部及![]() 上的点构成的圆弧长等于该圆周长的一半,求
上的点构成的圆弧长等于该圆周长的一半,求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的取值范围;
的取值范围;
(3)若曲线![]() (
(![]() )上的点都在
)上的点都在![]() 的外部,求
的外部,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)直线![]() 上点都在
上点都在![]() 的外部等价于不等式
的外部等价于不等式![]() 的解为一切实数,转化为恒成立问题从而求解;
的解为一切实数,转化为恒成立问题从而求解;
(2)根据对称性,只需要考虑这两个曲线在第一象限及![]() 、
、![]() 轴正半轴的情况,由此可得两曲线的交点坐标为
轴正半轴的情况,由此可得两曲线的交点坐标为![]() ,将点
,将点![]() 和
和![]() 代入双曲线得到两个方程,然后将
代入双曲线得到两个方程,然后将![]() 看成已知数,解出
看成已知数,解出![]() ,根据
,根据![]() ,解出
,解出![]() 的范围;
的范围;
(3)先将曲线![]() (
(![]() )转化为
)转化为![]() ,根据所有点都在
,根据所有点都在![]() 的外部,可以得到不等式
的外部,可以得到不等式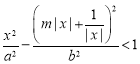 对任意非零实数
对任意非零实数![]() 均成立,令
均成立,令![]() ,转化为函数进行分类讨论,求解最值,从而得出
,转化为函数进行分类讨论,求解最值,从而得出![]() 的取值范围.
的取值范围.
解:(1)由题意,因为直线![]() 上点都在
上点都在![]() 的外部,
的外部,
所以直线![]() 上点
上点![]() 满足
满足![]() ,
,
即求不等式![]() 的解为一切实数时
的解为一切实数时![]() 的取值范围.
的取值范围.
对于不等式![]() ,
,
当![]() 时,不等式的解集不为一切实数,
时,不等式的解集不为一切实数,
于是有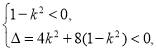 解得
解得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(2)因为圆![]() 和双曲线
和双曲线![]() 均关于坐标轴和原点对称,
均关于坐标轴和原点对称,
所以只需考虑这两个曲线在第一象限及![]() 、
、![]() 轴正半轴的情况.
轴正半轴的情况.
由题设,圆与双曲线的交点平分该圆在第一象限内的圆弧,
它们交点的坐标为![]() .
.
将![]() ,
,![]() 代入双曲线
代入双曲线![]() 方程,
方程,
得![]() (*),
(*),
又因为![]() 过点
过点![]() ,
,
所以![]() ,
,
将![]() 代入(*)式,
代入(*)式,
得![]() .
.
由![]() ,
,
解得![]() .
.
因此,![]() 的取值范围为
的取值范围为![]() .
.
(3)由![]() ,
,
得![]() .
.
将![]() 代入
代入![]() ,
,
因为曲线![]() (
(![]() )上的点都在
)上的点都在![]() 的外部,
的外部,
所以不等式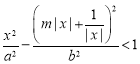 对任意非零实数
对任意非零实数![]() 均成立,
均成立,
其中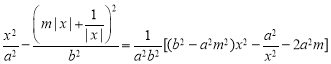 .
.
令![]() ,设
,设![]() ,(
,(![]() ).
).
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 不恒成立;
不恒成立;
当![]() 时,
时,![]() ,
,
函数![]() 的最大值为
的最大值为![]() ,
,
因为![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() .
.
综上,![]() ,解得
,解得![]() .
.
因此,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 经过曲线
经过曲线![]() 的焦点
的焦点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列![]() 的前n项和为
的前n项和为![]() 且满足
且满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 求正整数
求正整数![]() 的值;
的值;
(3)是否存在正整数![]() ,使得
,使得![]() 恰好为数列
恰好为数列![]() 的一项?若存在,求出所有满足条件的正整数
的一项?若存在,求出所有满足条件的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)已知数列![]() 满足
满足![]() (
(![]() ),首项
),首项![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)数列![]() 满足
满足![]() ,记数列
,记数列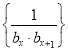 的前
的前![]() 项和为
项和为![]() ,
,![]() 是△ABC的内角,若
是△ABC的内角,若![]() 对于任意
对于任意![]() 恒成立,求角
恒成立,求角![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]() 在双曲线C上,设坐标原点为O.
在双曲线C上,设坐标原点为O.
(1)求双曲线C的方程;
(2)若过点![]() 的直线l与双曲线C交于R、S两点,若
的直线l与双曲线C交于R、S两点,若![]() ,求直线l的方程;
,求直线l的方程;
(3)设![]() 在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得
在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得![]() ?若存在,求出点T的坐标;若不存在,说明理由.
?若存在,求出点T的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,若对任意正整数n,总存在正整数m,使得
,若对任意正整数n,总存在正整数m,使得![]() ,则称
,则称![]() 是“H数列”;
是“H数列”;
(1)若数列![]() 的前n项和
的前n项和![]() (
(![]() ),判断数列
),判断数列![]() 是否是“H数列”?若是,给出证明;若不是,说明理由;
是否是“H数列”?若是,给出证明;若不是,说明理由;
(2)设数列![]() 是常数列,证明:
是常数列,证明:![]() 为“H数列”的充要条件是
为“H数列”的充要条件是![]() ;
;
(3)设![]() 是等差数列,其首项
是等差数列,其首项![]() ,公差
,公差![]() ,若
,若![]() 是“H数列”,求d的值;
是“H数列”,求d的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)![]() 是函数数
是函数数![]() 的导函数,记
的导函数,记![]() ,若
,若![]() 在区间
在区间![]() 上为单调函数,求实数a的取值范围;
上为单调函数,求实数a的取值范围;
(2)设实数![]() ,求证:对任意实数
,求证:对任意实数![]()
![]() ,总有
,总有![]() 成立.
成立.
附:简单复合函数求导法则为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com