
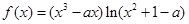 (
(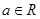 )
)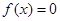 有3个不同的根,求实数
有3个不同的根,求实数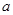 的取值范围;
的取值范围;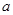 ,使得
,使得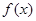 在
在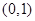 上恰有两个极值点
上恰有两个极值点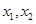 ,且满足
,且满足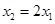 ,若存在,求实数
,若存在,求实数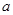 的值,若不存在,说明理由.
的值,若不存在,说明理由. ;(2)不存在,参考解析
;(2)不存在,参考解析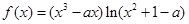 (
(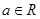 ),若方程
),若方程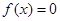 有3个不同的根,则可得到
有3个不同的根,则可得到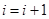 或
或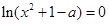 对两个方程分别讨论即可到结论.
对两个方程分别讨论即可到结论.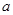 ,使得
,使得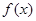 在
在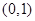 上恰有两个极值点
上恰有两个极值点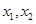 ,通过对函数求导,判断导函数的根的情况,通过换元使得等式简洁些.要满足
,通过对函数求导,判断导函数的根的情况,通过换元使得等式简洁些.要满足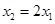 ,由于
,由于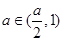 ,所以可得
,所以可得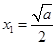 ,通过验证根是否存在.即可得到结论.
,通过验证根是否存在.即可得到结论.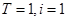 得:
得: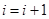 或
或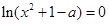
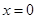 或
或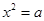 且
且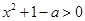
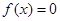 有3个不同的根,
有3个不同的根,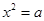 有两个不同的根
有两个不同的根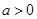
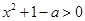 ,且要保证
,且要保证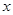 能取到0∴
能取到0∴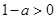 即
即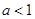
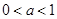 .
.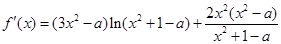
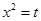 ,设
,设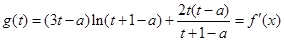
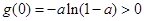
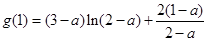 ∵
∵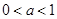 ∴
∴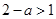 ∴
∴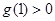
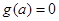
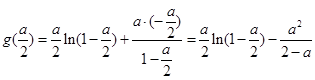
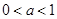 ∴
∴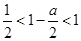 ,
,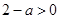 ∴
∴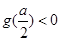
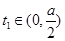 ,使得
,使得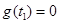 ,另外有
,另外有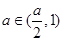 ,使得
,使得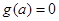
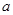 ,使得
,使得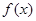 在
在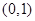 上恰有两个极值点
上恰有两个极值点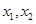 ,且满足
,且满足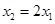
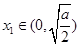 ,使得
,使得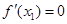 ,另外有
,另外有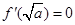 ,即
,即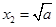
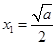 ,∴
,∴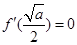 ,即
,即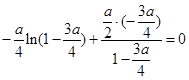
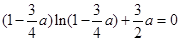 (*)
(*)
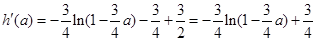
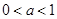 ∴
∴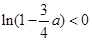
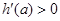 ∴
∴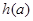 在
在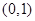 上是增函数
上是增函数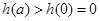
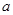 ,使得
,使得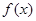 在
在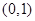 上恰有两个极值点
上恰有两个极值点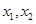 ,且满足
,且满足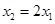


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:不详 题型:单选题
| A.[1,4] | B.[2,5] | C.[1,5] | D.[-5,-1] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com