
| A. | 3 | B. | -1 | C. | $1+2\sqrt{3}$ | D. | $1-2\sqrt{3}$ |
分析 利用单项式乘多项式展开数量积,再由数量积公式运算得答案.
解答 解:∵$\overrightarrow{a},\overrightarrow{b}$是单位向量,且它们的夹角为1200,
∴$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{4b})$=$|\overrightarrow{a}{|}^{2}-4|\overrightarrow{a}||\overrightarrow{b}|cos120°$
=$1-4×1×1×(-\frac{1}{2})$=3.
故选:A.
点评 本题考查平面向量的夹角、单位向量及数量积的运算,是基础题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:填空题
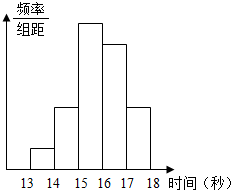 某年级200名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果以1为组距分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积依次为0.05,0.15,0.35,x,0.15,那么x=0.30;早这次百米测试中,成绩大于等于17秒的学生人数为30.
某年级200名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果以1为组距分成5组:[13,14),[14,15),[15,16),[16,17),[17,18],得到如图所示的频率分布直方图.如果从左到右的5个小矩形的面积依次为0.05,0.15,0.35,x,0.15,那么x=0.30;早这次百米测试中,成绩大于等于17秒的学生人数为30.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | -$\frac{7\sqrt{2}}{10}$ | D. | $\frac{7\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | e2 | C. | e | D. | $\frac{e}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5,6} | B. | {1,3,5} | C. | {2,3,4} | D. | {1,2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:?x∈R,x2≠x的否定是:?x0∈R,使得x02≠x | |
| B. | 命题:若x≥2且y≥3,则x+y≥5的否命题为:若x<2且y<3,则x+y<5 | |
| C. | 若ω=1是函数f(x)=cosωx在区间[0,π]上单调递减的充分不必要条件 | |
| D. | 命题:?x0∈R,x02+a<0为假命题,则实数a的取值范围是a>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
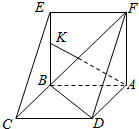 如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.
如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com