
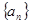 满足
满足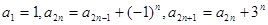 (
(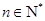 ).
).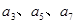 的值;
的值;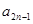 (用含
(用含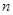 的式子表示);
的式子表示);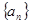 的前
的前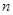 项和为
项和为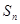 ,求
,求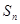 (用含
(用含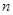 的式子表示).
的式子表示). ;(2)
;(2) ;
; .
. ;(2)从(1)中特殊值可能看不到数列
;(2)从(1)中特殊值可能看不到数列 的项有什么规律,但题中要求
的项有什么规律,但题中要求 ,那我们看看能否找到此数列的项之间有什么递推关系呢?把已知条件
,那我们看看能否找到此数列的项之间有什么递推关系呢?把已知条件 ,代入
,代入 即得
即得 ,由这个递推关系可采取累加的方法求得
,由这个递推关系可采取累加的方法求得 ;(3)要求数列
;(3)要求数列 的
的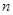 项和,在(2)基础上我们还必须求出偶数项
项和,在(2)基础上我们还必须求出偶数项 的表达式,这个根据已知易得,由于奇数项与偶数项的表达式不相同,因此在求
的表达式,这个根据已知易得,由于奇数项与偶数项的表达式不相同,因此在求 时,应该采取分组求和的方法,奇数项放在一起,偶数项放在一起,这就引起了分类讨论,要按
时,应该采取分组求和的方法,奇数项放在一起,偶数项放在一起,这就引起了分类讨论,要按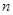 的奇偶来分类,确定
的奇偶来分类,确定 的最后一项
的最后一项 是项还是偶数项,这样分组才能明确.
是项还是偶数项,这样分组才能明确.
 (
(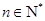 ),
),
 .
. .
. .
. ,
, .
. .
. ,
, 当
当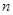 为偶数时,
为偶数时,
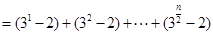
 .
.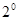 当
当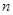 为奇数时,
为奇数时,

 .
.
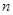 项和与分组求和.
项和与分组求和.

科目:高中数学 来源:不详 题型:解答题
 中的
中的 、
、 、
、 .
. 的通项公式;
的通项公式; 的前n项和为
的前n项和为 ,求证:数列
,求证:数列 是等比数列.
是等比数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com