
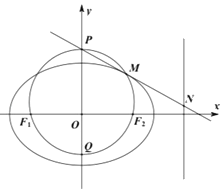
【题目】如图,点M在椭圆![]() 1(0<b
1(0<b![]() )上,且位于第一象限,F1,F2为椭圆的两个焦点,过F1,F2,M的圆与y轴交于点P,Q(P在Q的上方),|OP||OQ|=1.
)上,且位于第一象限,F1,F2为椭圆的两个焦点,过F1,F2,M的圆与y轴交于点P,Q(P在Q的上方),|OP||OQ|=1.
(Ⅰ)求b的值;
(Ⅱ)直线PM与直线x=2交于点N,试问,在x轴上是否存在定点T,使得![]()
![]() 为定值?若存在,求出点T的坐标与该定值;若不存在,请说明理由.
为定值?若存在,求出点T的坐标与该定值;若不存在,请说明理由.
【答案】(Ⅰ)1(Ⅱ)存在定点T(1,0),使得![]()
![]() 为定值0.
为定值0.
【解析】
(I)设圆心![]() .则圆的方程为:
.则圆的方程为:![]() ,令
,令![]() ,得:
,得:![]() ,即可得出
,即可得出![]() ,进而得出.
,进而得出.
(II)设![]() .将
.将![]() 代入圆与椭圆的方程,可得
代入圆与椭圆的方程,可得![]() 坐标,可得直线
坐标,可得直线![]() 的方程,设
的方程,设![]() ,可得
,可得![]()
![]() ,即可得出.
,即可得出.
(I)设圆心(0,t).则圆的方程为:x2+(y﹣t)2=c2+t2.
令x=0,得:y2﹣2ty﹣c2=0(*),
∴|OP||OQ|=|yPyQ|=c2=1.
∴b=a2﹣c2=1.
(II)设M(x0,y0).![]()
将M(x0,y0)代入圆与椭圆的方程,可得:![]() 2ty0﹣1=0,
2ty0﹣1=0,![]() 2
2![]() 2,消去x0,
2,消去x0,
得t![]() ,代入(*)得:y2
,代入(*)得:y2![]() 1=0,
1=0,
即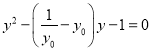 ,所以
,所以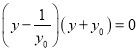
过F1,F2,M的圆与y轴交于点P,Q(P在Q的上方).
所以yP![]() ,
,![]() .
.
则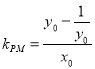 .
.
则直线![]() 的方程为:y
的方程为:y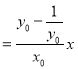
![]() ,
,
由直线PM与![]() 的交点为
的交点为![]() .
.
所以在直线PM的方程中,令![]() 得,
得,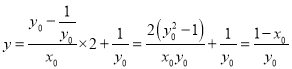 .
.
得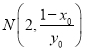
设T(d,0),![]()
![]() (x0﹣d,y0)(2﹣d,
(x0﹣d,y0)(2﹣d,![]() )
)
=(x0﹣d)(2﹣d)+1﹣x0=(1﹣d)x0﹣d(2﹣d)+1.
要使得![]()
![]() 为定值,即与M的坐标无关.
为定值,即与M的坐标无关.
当d=1时,![]()
![]() 0为定值.
0为定值.
存在定点T(1,0),使得![]()
![]() 为定值0.
为定值0.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
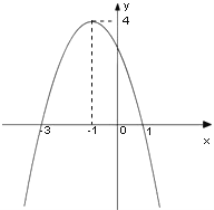
【题目】如图是一个二次函数y=f(x)的图象
(1)写出这个二次函数的零点
(2)求这个二次函数的解析式
(3)当实数k在何范围内变化时,函数g(x)=f(x)-kx在区间[-2,2]上是单调函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x﹣y+3=0和l2:x+y+1=0的交点为A,过A且与x轴和y轴都相切的圆的方程为_____,动点B,C分别在l1和l2上,且|BC|=2,则过A,B,C三点的动圆扫过的区域的面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在创建“全国文明卫生城市”过程中,某市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次).通过随机抽样,得到参加问卷调查的![]() 人的得分(满分100分)统计结果如下表所示:
人的得分(满分100分)统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)由频数分布表可以大致认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求
人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求![]()
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) |
|
|
概率 |
|
|
现有市民甲参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与均值.
的分布列与均值.
附:参考数据与公式![]()
若![]() ,则
,则![]() =0.9544,
=0.9544,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,正确命题的序号为 (写出所有正确命题的序号).
①函数![]() 的最小值为
的最小值为![]() ;
;
②已知定义在![]() 上周期为4的函数
上周期为4的函数![]() 满足
满足![]() ,则
,则![]() 一定为偶函数;
一定为偶函数;
③定义在![]() 上的函数
上的函数![]() 既是奇函数又是以2为周期的周期函数,则
既是奇函数又是以2为周期的周期函数,则![]() ;
;
④已知函数![]() ,则
,则![]() 是
是![]() 有极值的必要不充分条件;
有极值的必要不充分条件;
⑤已知函数![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上.
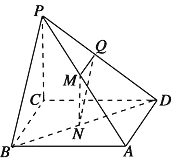
(1)若PM:MA=BN:ND=PQ:QD,求证:平面MNQ∥平面PBC.
(2)若Q满足PQ:QD=2,则M点满足什么条件时,BM∥面AQC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com