
【题目】2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的![]() ;人口总数约为32.1亿,占全球总人口的
;人口总数约为32.1亿,占全球总人口的![]() ;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的
;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的![]() .
.
2016年“一带一路”沿线国家情况
人口(万人) | GDP(亿美元) | 进口额(亿美元) | 出口额(亿美元) | |
蒙古 | 301.4 | 116.5 | 38.7 | 45.0 |
东南亚11国 | 63852.5 | 25802.2 | 11267.2 | 11798.6 |
南亚8国 | 174499.0 | 29146.6 | 4724.1 | 3308.5 |
中亚5国 | 6946.7 | 2254.7 | 422.7 | 590.7 |
西亚、北非19国 | 43504.6 | 36467.5 | 9675.5 | 8850.7 |
东欧20国 | 32161.9 | 26352.1 | 9775.5 | 11388.4 |
关于“一带一路”沿线国家2016年状况,能够从上述资料中推出的是( )
A.超过六成人口集中在南亚地区
B.东南亚和南亚国家GDP之和占全球的![]() 以上
以上
C.平均每个南亚国家对外贸易额超过1000亿美元
D.平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额
【答案】C
【解析】
利用表中所给的数据对四个选项逐一判断即可.
A:南亚地区人口总数为174499.0万人,“一带一路”沿线国家人口总数为:321266.1万人,所以![]() ,故本选项说法不正确的;
,故本选项说法不正确的;
B:东南亚和南亚国家GDP之和54948.8亿美元,“一带一路”沿线国家GDP之和120139.6亿美元,所以![]() ,所以东南亚和南亚国家GDP之和占“一带一路”沿线国家GDP之和的
,所以东南亚和南亚国家GDP之和占“一带一路”沿线国家GDP之和的![]() ,因此东南亚和南亚国家GDP之和占全球的
,因此东南亚和南亚国家GDP之和占全球的![]() ,故本选项说法是不正确的;
,故本选项说法是不正确的;
C:南亚国家对外贸易额的平均值为:![]() ,故本选项说法是正确的;
,故本选项说法是正确的;
D:平均每个东欧国家的进口额为:![]() ,平均每个西亚、北非国家的进口额为:
,平均每个西亚、北非国家的进口额为:![]() ,故本选项说法是不正确的.
,故本选项说法是不正确的.
故选:C


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() (
(![]() ).
).
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由. (参考数据:
的最小值;若不存在,请说明理由. (参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】九龙坡区围绕大力发展高新技术产业、推进高质量城市管理、创造高品质人民生活,建设宜居、宜业、宜游的“三高九龙坡、三宜山水城”的总愿景,全面开启新时代的新梦想、新征程.热心网友“我是坡民”通过问卷,对近五年游客满意度排在前三名的区内景点进行了统计,结果如表一.根据此表,他又对游览过热门景点重庆动物园的100名游客进行满意度调查,给景点打分,满分为100分,得分超过90分的为“特别满意”,其余为“基本满意”,将受调查游客年龄为12岁及以下的人群称为儿童,得到![]() 列联表,如表二:
列联表,如表二:
表一:
年份景点排名 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
1 | 重庆动物园 | 重庆动物园 | 龙门阵景区 | 彩云湖 | 彩云湖 |
2 | 华岩景区 | 华岩景区 | 重庆动物园龙 | 龙门阵景区 | 黄桷坪涂鸦街 |
3 | 巴国城 | 海兰云天 | 黄桷坪涂鸦街 | 华岩景区 | 重庆动物园 |
表二:
特别满意 | 基本满意 | 合计 | |
儿童 | 40 | ||
非儿童 | 30 | ||
合计 | 60 | 100 |
(1)完成表二的列联表,并判断是否有99.9%的把握认为调查对象是否“特别满意”与是否是儿童有关;
(2)为安排节假日出行,“我是坡民”从表一的5个年份中随机选择2个年份,再从这2个年份排名前三的景点中任意选择1个景点,记选择出的景点中“重庆动物园”出现的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆,运送这批水果的费用最少为( )
A.2400元B.2560元C.2816元D.4576元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
,![]() ,点P满足
,点P满足![]() .
.
(1)求点P的轨迹C的方程;
(2)若![]() ,直线l与轨迹C交于A,B两点,
,直线l与轨迹C交于A,B两点,![]() ,
,![]() 的斜率之和为2,问直线l是否恒过定点,若过定点,求出定点的坐标;若不过定点,请说明理由.
的斜率之和为2,问直线l是否恒过定点,若过定点,求出定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]() 满足:
满足:![]() ,且对任意正整数
,且对任意正整数![]() ,
,![]() 为前
为前![]() 项
项![]() ,
,![]() ,…,
,…,![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(1)直接写出![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)求证:该数列中存在无穷项的值为1;
(3)已知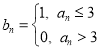 ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 经过曲线
经过曲线![]() 的焦点
的焦点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某北方村庄4个草莓基地,采用水培阳光栽培方式种植的草莓个大味美,一上市便成为消费者争相购买的对象.光照是影响草莓生长的关键因素,过去50年的资料显示,该村庄一年当中12个月份的月光照量X(小时)的频率分布直方图如下图所示(注:月光照量指的是当月阳光照射总时长).
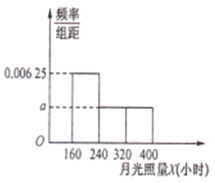
(1)求月光照量![]() (小时)的平均数和中位数;
(小时)的平均数和中位数;
(2)现准备按照月光照量来分层抽样,抽取一年中的4个月份来比较草莓的生长状况,问:应在月光照量![]() ,
,![]() ,
,![]() 的区间内各抽取多少个月份?
的区间内各抽取多少个月份?
(3)假设每年中最热的5,6,7,8,9,10月的月光照量![]() 是大于等于240小时,且6,7,8月的月光照量
是大于等于240小时,且6,7,8月的月光照量![]() 是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量
是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量![]() (小时)都不低于320的概率.
(小时)都不低于320的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,过
,过![]() 且与圆
且与圆![]() 相切的动圆圆心为
相切的动圆圆心为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知过点![]() 的两直线
的两直线![]() 和
和![]() 互相垂直,且直线
互相垂直,且直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点(
两点(![]() ,
,![]() ,
,![]() ,
,![]() 为不同的四个点),求四边形
为不同的四个点),求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com