
分析 由{x},[x],x成等比数列,可得[x]2={x}•x=(x-[x])•x,解出即可得出.
解答 解:∵{x},[x],x成等比数列,
∴[x]2={x}•x=(x-[x])•x,
解得[x]=$\frac{\sqrt{5}-1}{2}$x,
∵$\frac{\sqrt{5}-1}{2}$×$\frac{\sqrt{5}+1}{2}$=1.
∴可设x=k•$\frac{\sqrt{5}+1}{2}$(k∈N*).
∴$[\frac{\sqrt{5}+1}{2}k]$=k,
当k=1时,上式成立;
k≥2时,不成立.
∴x=$\frac{\sqrt{5}+1}{2}$.
故答案为:$\frac{\sqrt{5}+1}{2}$.
点评 本题考查了等比数列的通项公式及其性质、取整函数[x]的性质,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{a}$<x<1} | B. | {x|-1<x<$\frac{1}{a}$} | C. | {x|1$<x<\frac{1}{a}$} | D. | {x|-$\frac{1}{a}$<x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,6] | B. | [0,6] | C. | [$\frac{2}{3}$,6] | D. | [1,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
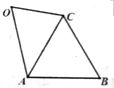 已知a,b,c分别是△ABC的内角A,B,C所对的边长,a=c,且满足bsinA=$\sqrt{3}$acosB.点O为△ABC外一点,OA=2OC=4,求平面四边形ABCO的面积的最大值.
已知a,b,c分别是△ABC的内角A,B,C所对的边长,a=c,且满足bsinA=$\sqrt{3}$acosB.点O为△ABC外一点,OA=2OC=4,求平面四边形ABCO的面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com