
【题目】在数列{an}中,a1=1,Sn+1=4an+2,则a2013的值为( )
A.3019×22012
B.3019×22013
C.3018×22012
D.无法确定
【答案】A
【解析】解:∵在数列{an}中,a1=1,Sn+1=4an+2,
∴S2=4a1+2=a1+a2 , ∴a2=3a1+2=5,
a1+a2+…+an+1=4an+2,①
a1+a2+…+an=4an﹣1+2,②
①﹣②,得:an+1=4an﹣4an﹣1 ,
an+1﹣2an=2(an﹣2an﹣1),
∴{an﹣2an﹣1}是等比数列,公比q=2,
an﹣2an﹣1=2n﹣2(a2﹣2a1)=32n﹣2 ,
∴ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴{ ![]() }是等差数列,公差d=
}是等差数列,公差d= ![]() ,n≥2,
,n≥2,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∴an=(3n﹣1)2n﹣2 ,
,∴an=(3n﹣1)2n﹣2 ,
∴a2013=(3×2013﹣1)22011=3019×22012 .
故选:A.
【考点精析】解答此题的关键在于理解数列的通项公式的相关知识,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】设点P(x,y)是曲线a|x|+b|y|=1(a≥0,b≥0)上任意一点,其坐标(x,y)均满足 ![]() ,则
,则 ![]() a+b取值范围为( )
a+b取值范围为( )
A.(0,2]
B.[1,2]
C.[1,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,离心率等于 ![]() ,它的一个短轴端点恰好是抛物线x2=8
,它的一个短轴端点恰好是抛物线x2=8 ![]() y的焦点.
y的焦点.
(1)求椭圆C的方程;
(2)已知P(2,m)、Q(2,﹣m)(m>0)是椭圆上的两点,A,B是椭圆上位于直线PQ两侧的动点,
①若直线AB的斜率为 ![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得﹣200分).设每次击鼓出现音乐的概率为 ![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列和数学期望E(X).
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD,B1为PB的中点,D1为PD的中点,则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比是( ) 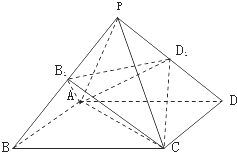
A.1:4
B.3:8
C.1:2
D.2:3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 ![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com