
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1 , CC1上,且C1F= ![]() C1C,BE=λBB1 , 0<λ<1.
C1C,BE=λBB1 , 0<λ<1. 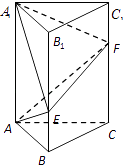
(1)当λ= ![]() 时,求异面直线AE与A1F所成角的大小;
时,求异面直线AE与A1F所成角的大小;
(2)当直线AA1与平面AEF所成角的正弦值为 ![]() 时,求λ的值.
时,求λ的值.
【答案】
(1)解:建立如图所示的空间直角坐标系A﹣xyz.
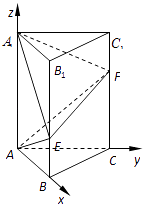
因为AB=AC=1,AA1=3, ![]() ,
,
所以各点的坐标为A(0,0,0),E(1,0,1),A1(0,0,3),
F(0,1,2). ![]() ,
, ![]() .因为
.因为 ![]() ,
, ![]() ,
,
所以 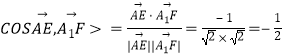 .所以向量
.所以向量 ![]() 和
和 ![]() 所成的角为120°,
所成的角为120°,
所以异面直线AE与A1F所成角为60°.
(2)解:因为E(1,0,3λ),F(0,1,2),所以 ![]() .
.
设平面AEF的法向量为n=(x,y,z),
则 ![]() ,且
,且 ![]() .
.
即x+3λz=0,且y+2z=0.令z=1,则x=﹣3λ,y=﹣2.
所以 ![]() =(﹣3λ,﹣2,1)是平面AEF的一个法向量.
=(﹣3λ,﹣2,1)是平面AEF的一个法向量.
又 ![]() ,则
,则 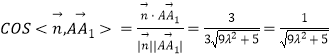 ,
,
又因为直线AA1与平面AEF所成角的正弦值为 ![]() ,
,
所以 ![]() =
= ![]() ,解得,
,解得, ![]()
【解析】建立如图所示的空间直角坐标系A﹣xyz.(1)推出相关点的坐标,求出向量 ![]() 和
和 ![]() 对应的向量,利用向量的数量积求出夹角即可.(2)求出平面AEF的法向量,
对应的向量,利用向量的数量积求出夹角即可.(2)求出平面AEF的法向量, ![]() ,利用向量的数量积求解直线AA1与平面AEF所成角的正弦值为
,利用向量的数量积求解直线AA1与平面AEF所成角的正弦值为 ![]() ,得到
,得到 ![]() .
.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则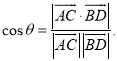 .
.


科目:高中数学 来源: 题型:
【题目】已知正三角形内切圆的半径是高的 ![]() ,把这个结论推广到正四面体,类似的结论正确的是( )
,把这个结论推广到正四面体,类似的结论正确的是( )
A.正四面体的内切球的半径是高的 ![]()
B.正四面体的内切球的半径是高的 ![]()
C.正四面体的内切球的半径是高的 ![]()
D.正四面体的内切球的半径是高的 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用计算机随机产生的有序二元数组(x,y)满足﹣1≤x≤1,﹣1≤y≤1.
(1)若x,y∈Z,求事件“x2+y2≤1”的概率.
(2)求事件“x2+y2>1”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=a ![]() ﹣nan+1,且a1=2.
﹣nan+1,且a1=2.
(1)计算a2 , a3 , a4的值,由此猜想数列{an}的通项公式,并用数学归纳法证明;
(2)求证:2nn≤a ![]() <3nn .
<3nn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,an+1= ![]() (n=1,2,3,…),
(n=1,2,3,…),
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的图象过点(﹣1,2),且在点(﹣1,f(﹣1))处的切线与直线x﹣5y+1=0垂直.
的图象过点(﹣1,2),且在点(﹣1,f(﹣1))处的切线与直线x﹣5y+1=0垂直.
(1)求实数b,c的值;
(2)求f(x)在[﹣1,e](e为自然对数的底数)上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)上任意一点到两焦点距离之和为
=1(a>b>0)上任意一点到两焦点距离之和为 ![]() ,离心率为
,离心率为 ![]() ,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
(1)求椭圆E的标准方程;
(2)证明:直线PQ与直线OQ的斜率之积是定值;
(3)证明:直线PQ与椭圆E只有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P. 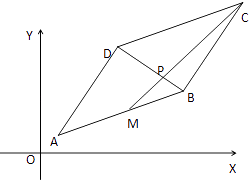
(1)求直线CM的方程;
(2)求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com