
分析 利用函数性质及对数运算法则求解.
解答 解:∵函数$f(x)=\frac{{{e^{2x}}-1}}{{{e^{2x}}+1}}+x+1$,
∴$f(ln3)+f(ln\frac{1}{3})$=$\frac{{e}^{2ln3}-1}{{e}^{2ln3}+1}$+ln3+1+$\frac{{e}^{2ln\frac{1}{3}}-1}{{e}^{2ln\frac{1}{3}}+1}$+ln$\frac{1}{3}$+1
=$\frac{{e}^{ln9}-1}{{e}^{ln9}+1}$+$\frac{-{e}^{ln9}-1}{-{e}^{ln9}+1}$+ln3-ln3+2
=$\frac{8}{10}+\frac{-10}{-8}$+2
=$\frac{81}{20}$.
故答案为:$\frac{81}{20}$.
点评 本题考查函数值的求法,是基础题,解题是要认真审题,注意函数性质的合理运用.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
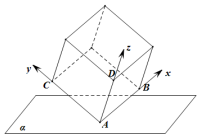 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{13}$ | B. | -$\frac{12}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 第x月 | 1 | 2 | 3 | 4 | 5 | 6 |
| 枝数y(枝) | 2 | 4 | 7 | 16 | 33 | 63 |
| A. | y=2x | B. | y=x2-x+2 | C. | y=2x | D. | y=log2x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小项为-1,最大项为3 | B. | 最小项为-1,无最大项 | ||
| C. | 无最小项,最大项为3 | D. | 既无最小项,也无最大项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com