
【题目】若a、b是方程2(lg x)2-lg x6+3=0的两个实根,求lg(ab)·(logab+logba)的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知幂函数![]() (m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(1)求函数f(x)的解析式;
(2)设函数![]() ,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥C﹣OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2 ![]() ,D为AB的中点.
,D为AB的中点. 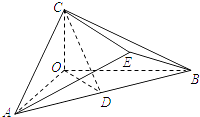
(Ⅰ)求证:AB⊥平面COD;
(Ⅱ)若动点E满足CE∥平面AOB,问:当AE=BE时,平面ACE与平面AOB所成的锐二面角是否为定值?若是,求出该锐二面角的余弦值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂今年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量)x(万件)与年促销费m(万元)(m≥0)满足x=3-![]() .已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将今年该产品的利润y(万元)表示为年促销费m(万元)的函数;
(2)求今年该产品利润的最大值,此时促销费为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若f(x)在区间(﹣∞,2]上是减函数,且对任意的x∈[1,a+1],总有f(x)≤0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体PABCD的直观图及三视图如图所示,E、F分别为PC、BD的中点.

(I)求证:EF∥平面PAD;
(II)求证:平面PDC⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com