
 ,
,


 ,
,
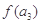 =
= ,则
,则 ;
; .
.  ,
,


 ,且
,且
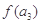 =
= ,
, =α,则a1=α-,
=α,则a1=α-, ,
,
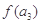 =
= ,
, =α=.
=α=. 2(
2( +
+ ……+
……+ )-(cos
)-(cos +cos
+cos +cos
+cos +cosπ+cos
+cosπ+cos +cos
+cos +cos
+cos +cos2π+cos
+cos2π+cos +cos
+cos )=
)= .
.

科目:高中数学 来源:不详 题型:解答题
 .
.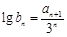 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 米,
米, 米,
米, 米,…,
米,…, 米或
米或 米;
米; 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.
秒. 米(允许超出
米(允许超出 米)所需的最少时间是【 】.
米)所需的最少时间是【 】.A. 秒 秒 | B. 秒 秒 | C. 秒 秒 | D. 秒 秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com