���𰸡�
��������I����������P�Ķ����жϳ���������P�ļ��ϣ����ü���S��T�Ķ���д��S��T��
��II���ݾ�������P�ļ�������a��A������-a∉A���õ�0∉A�õ���a
i��a
i��∉T������a
i��a
j����Tʱ����a
j��a
i��∉T�����T�е�Ԫ�ظ�����
��III����ӦS�е�Ԫ�ؾ�S��T�Ķ���õ�Ҳ��T�е�Ԫ�أ���֮����T�е�Ԫ��Ҳ��s�е�Ԫ�أ��õ����������е�Ԫ����ͬ��
�����I���⣺����{0��1��2��3}����������P��
����{-1��2��3}��������P������Ӧ�ļ���S��T��
S=��-1��3������3��-1����T=��2��-1������2��3����
��II��֤�������ȣ���A��Ԫ�ع��ɵ��������ԣ�a
i��a
j������k
2����
��Ϊ0∉A�����ԣ�a
i��a
i��∉T��i=1��2����k����
����Ϊ��a��Aʱ��-a∉Aʱ��-a∉A��
���Ե���a
i��a
j����Tʱ����a
j��a
i��∉T��i��j=1��2����k����
�Ӷ�������T��Ԫ�صĸ������Ϊ
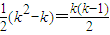
��
��
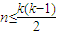
��
��III���⣺m=n��֤�����£�
��1�����ڣ�a��b����S�����ݶ��壬
a��A��b��A����a+b��A���Ӷ���a+b��b����T��
�����a��b���루c��d����S�IJ�ͬԪ�أ�
��ôa=c��b=d��������һ����������
�Ӷ�a+b=c+d��b=d��Ҳ������һ����������
�ʣ�a+b��b���루c+d��d��Ҳ��T�IJ�ͬԪ�أ�
�ɼ���S��Ԫ�صĸ���������T��Ԫ�صĸ�������m��n��
��2�����ڣ�a��b����T�����ݶ��壬a��A��b��A��
��a-b��A���Ӷ���a-b��b����S��
�����a��b���루c��d����T�IJ�ͬԪ�أ�
��ôa=c��b=d��������һ����������
�Ӷ�a-b=c-d��b=d��Ҳ��������һ����������
�ʣ�a-b��b���루c-d��d��Ҳ��S�IJ�ͬԪ�أ�
�ɼ���T��Ԫ�صĸ���������S��Ԫ�صĸ�������n��m��
�ɣ�1����2����֪��m=n��
���������⿼���������е��¶�����⣻�¶������ǽ����곣�������ͣ�Ҫ���ӣ�

 ��
�� ��
�� ��
��

