在△ABC中，已知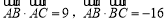
．求：
（1）AB的值；（2）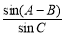
的值．
小学教材全测系列答案科目：高中数学 来源：2013-2014学年江苏省徐州市高三第三次质量检测文科数学试卷（解析版） 题型：解答题
根据统计资料，某工艺品厂的日产量最多不超过20件，每日产品废品率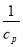
与日产量
(件)之间近似地满足关系式
(日产品废品率
)．已知每生产一件正品可赢利2千元，而生产一件废品则亏损1千元．（该车间的日利润
日正品赢利额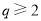
日废品亏损额）
（1）将该车间日利润
(千元)表示为日产量
(件)的函数；
（2）当该车间的日产量为多少件时，日利润最大？最大日利润是几千元？
查看答案和解析>>
科目：高中数学 来源：2013-2014学年江苏省高考模拟考试文科数学试卷（解析版） 题型：解答题
给定椭圆
，称圆心在坐标原点O，半径为
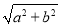的圆是椭圆C的“伴随圆”，已知椭圆C的两个焦点分别是
.
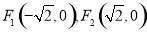（1）若椭圆C上一动点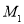
满足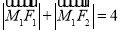
，求椭圆C及其“伴随圆”的方程；
（2）在（1）的条件下，过点
作直线l与椭圆C只有一个交点，且截椭圆C的“伴随圆”所得弦长为
，求P点的坐标；
（3）已知
，是否存在a，b，使椭圆C的“伴随圆”上的点到过两点
的直线的最短距离
.若存在，求出a，b的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年江苏省南通市高三第二次调研测试数学试卷（解析版） 题型：解答题
设函数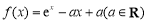
，其图象与
轴交于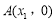
，
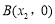两点，且x1＜x2．
（1）求
的取值范围；
（2）证明：
（
为函数
的导函数）；
（3）设点C在函数
的图象上，且△ABC为等腰直角三角形，记
，求
的值．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷（解析版） 题型：填空题
在平面直角坐标系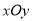
中，圆C的方程为
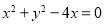．若直线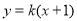
上存在一点
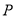，使过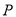
所作的圆的两条切线相互垂直，则实数
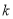的取值范围是 ．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷（解析版） 题型：解答题
某种树苗栽种时高度为A(A为常数)米，栽种n年后的高度记为f(n)．经研究发现f(n)近似地满足 f(n)＝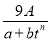
，其中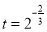
，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍．
（1）栽种多少年后，该树木的高度是栽种时高度的8倍；
（2）该树木在栽种后哪一年的增长高度最大．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
;（2）
．
，可联想到向量运算法则得：
，即可解得所求的长
;（2）对于所求
，不难想到可将其运用两角差的正弦三角公式展开得：
，在三角形中观察此式结构特征可想到运用正弦定理化简得：
，此时可联系（1）中所给向量数量积的定义进而可得：
，边
，即
，故
． 14分
.
的值为 ．
（其中i为虚数单位）的模为 ．