
【题目】数列![]() 满足
满足![]() ,
,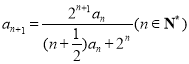 .
.
(1)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)由已知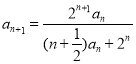 ,得
,得 ,
,
即![]() ,即
,即![]() ,即
,即![]() .(2分)
.(2分)
所以![]() ,
,![]() ,…,
,…,![]() ,
,
以上各式相加得![]() .
.
又![]() ,所以
,所以![]() .(5分)
.(5分)
(2)由(1)知![]() ,所以
,所以![]() ,
,
![]()
![]()
![]()
![]() .(7分)
.(7分)
所以![]()
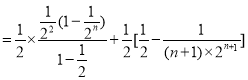
![]()
![]() .(10分)
.(10分)
【易错提醒】(1)对递推式变形时,应明确方向,准确把握数列的递推关系,通过变形将其转化为常见的等差、等比数列问题求解是解决此类问题的基本思路;(2)构造新数列时,一定要注意原数列的项与新数列的项之间的对应,如本题中第(1)问,![]() ,则
,则![]() 的表达式既不是
的表达式既不是![]() ,也不是
,也不是![]() ,而是
,而是![]() ,即把式子中所有的
,即把式子中所有的![]() 都换成
都换成![]() .
.
【解题技巧】求解数列递推关系式问题的基本原则就是对数列的递推式进行变换,把原问题转换为等差、等比数列进行处理.转化的常用方法有:(1)待定系数法,如![]() ,可以通过待定系数
,可以通过待定系数![]() 将其转化为形如
将其转化为形如![]() 的等比数列;(2)取倒数法,如本题;(3)观察变换法,如
的等比数列;(2)取倒数法,如本题;(3)观察变换法,如![]() ,可以在两端同时除以
,可以在两端同时除以![]() ,转化为形如
,转化为形如![]() 的等差数列;(4)取对数法等.求解数列递推关系式问题要注意选取合适的变换递推式的方法,通过变换进行解答,在变换时要小心谨慎.
的等差数列;(4)取对数法等.求解数列递推关系式问题要注意选取合适的变换递推式的方法,通过变换进行解答,在变换时要小心谨慎.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若PF=3,且双曲线的离心率e=![]() ,求该双曲线的方程.
,求该双曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,若E是AB的中点,P是△ABC(包括边界)内任一点.则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣6,6]
B.[﹣9,9]
C.[0,8]
D.[﹣2,6]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题: 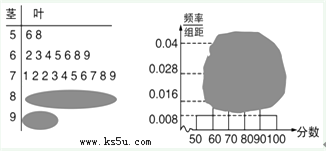
(1)求参加数学抽测的人数n、抽测成绩的中位数及分数分别在[80,90),[90,100]内的人数;
(2)若从分数在[80,100]内的学生中任选两人进行调研谈话,求恰好有一人分数在[90,100]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxcosx+2 ![]() cos2x﹣
cos2x﹣ ![]()
(1)求函数f(x)的最小正周期和单调减区间;
(2)已知△ABC的三个内角A,B,C的对边分别为a,b,c,其中a=7,若锐角A满足f( ![]() ﹣
﹣ ![]() )=
)= ![]() ,且sinB+sinC=
,且sinB+sinC= ![]() ,求bc的值.
,求bc的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别为a,b,c,B= ![]() .
.
(1)若a=3,b= ![]() ,求c的值;
,求c的值;
(2)若f(A)=sinA( ![]() cosA﹣sinA),a=
cosA﹣sinA),a= ![]() ,求f(A)的最大值及此时△ABC的外接圆半径.
,求f(A)的最大值及此时△ABC的外接圆半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com