
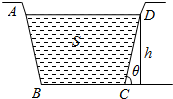
 如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周.
如图,水渠的横断面为等腰梯形,水的横断面面积为S,水面高为h,问侧面与地面所成角θ为多大时,横断面被水浸湿的长度(称为湿周)最小?并求出最小湿周. 分析 设横断面被水浸湿的长度为l,AB=CD=x,可得l=$\frac{S}{h}$-(2-cosθ)•$\frac{h}{sinθ}$,导数法求到唯一的极值即为所求.
解答 解:设横断面被水浸湿的长度为l,AB=CD=x,
则l=BC+2x=$\frac{S}{h}$-xcosθ+2x=$\frac{S}{h}$-(2-cosθ)x
=$\frac{S}{h}$-(2-cosθ)•$\frac{h}{sinθ}$,
令l′=0,即$\frac{1-2cosθ}{si{n}^{2}θ}$,解得cosθ=$\frac{1}{2}$,θ=60°,
∵l只有1个极值点,也是最小值点,
把θ=60°代入l=$\frac{S}{h}$-(2-cosθ)•$\frac{h}{sinθ}$可得lmin=$\frac{S}{h}$+$\sqrt{3}$h,
∴当侧面与地面所成角θ=60°时,横断面被水浸湿的长度最小,且最小值为lmin=$\frac{S}{h}$+$\sqrt{3}$h,
点评 本题考查三角函数的最值,涉及三角形的边角关系和函数的极值,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a2014>a1007+a1008 | B. | a1+a2014<a1007+a1008 | ||
| C. | a1+a2014≥a1007+a1008 | D. | a1+a2014与a1007+a1008无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com