
【题目】椭圆 ![]() 过点
过点 ![]() ,离心率为
,离心率为 ![]() ,左、右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点. (Ⅰ)求椭圆C的方程;
,左、右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点. (Ⅰ)求椭圆C的方程;
(Ⅱ)当△F2AB的面积为 ![]() 时,求直线的方程.
时,求直线的方程.
【答案】解:(Ⅰ)∵椭圆 ![]() 过点
过点 ![]() , ∴
, ∴ ![]() ①,
①,
又∵离心率为 ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ②,
②,
联立①②得a2=4,b2=3.
∴椭圆的方程为: ![]()
(Ⅱ)①当直线的倾斜角为 ![]() 时,
时, ![]() ,
,![]() =
= ![]() =
= ![]() ,不适合题意.
,不适合题意.
②当直线的倾斜角不为 ![]() 时,设直线方程l:y=k(x+1),
时,设直线方程l:y=k(x+1),
代入 ![]() 得:(4k2+3)x2+8k2x+4k2﹣12=0
得:(4k2+3)x2+8k2x+4k2﹣12=0
设A(x1 , y1),B(x2 , y2),则 ![]() ,
, ![]() ,
,
∴|AB|= ![]() =
= 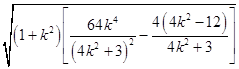 =
= ![]() .
.
点F2到直线l的距离d= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
化为17k4+k2﹣18=0,解得k2=1,∴k=±1,
∴直线方程为:x﹣y+1=0或x+y+1=0
【解析】(Ⅰ)由于椭圆 ![]() 过点
过点 ![]() ,离心率为
,离心率为 ![]() ,可得
,可得 ![]() ,
, ![]() 即
即 ![]() ,即可解出.(Ⅱ)对直线l的斜率分类讨论,与椭圆的方程联立可得根与系数的关系,再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出.
,即可解出.(Ⅱ)对直线l的斜率分类讨论,与椭圆的方程联立可得根与系数的关系,再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1 , ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题: (Ⅰ)求证:异面直线A1D与BC互相垂直;
(Ⅱ)求二面角(钝角)D﹣A1C﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a≥0,函数f(x)=(x2﹣2ax)ex , 若f(x)在[﹣1,1]上是单调减函数,则a的取值范围是( )
A.0<a< ![]()
B.![]() <a<
<a< ![]()
C.a≥ ![]()
D.0<a< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() 在
在 ![]() 内任取两个实数p,q,且p≠q,不等式
内任取两个实数p,q,且p≠q,不等式 ![]() 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
A.[﹣1,0]
B.[﹣1,+∞)
C.[0,3]
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)的定义域是(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<f'(x),则不等式 ![]() f(2)的解集是( )
f(2)的解集是( )
A.(﹣∞,2)∪(1,+∞)
B.(﹣2,1)
C.(﹣∞,﹣1)∪(2,+∞)
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com