
【题目】如图,矩形ABCD中,AB=1,BC=2,半圆O以BC为直径,平面ABCD垂直于半圆O所在的平面,P为半圆周上任意一点(与B、C不重合). 
(1)求证:平面PAC⊥平面PAB;
(2)若P为半圆周中点,求此时二面角P﹣AC﹣D的余弦值.
【答案】
(1)证明:∵半圆O以BC为直径,
∴PC⊥PB,
∵平面ABCD垂直于半圆O所在的平面,ABCD是矩形,
∴AB⊥底面BPC,则AB⊥PC,
∵AB∩BP=B,
∴PC⊥面PAB,
∵PC平面PAC,
∴平面PAC⊥平面PAB,
(2)解:连接OP,作OE垂直BC,建立以O为坐标原点,OP,OE,OC分别为x,y,z轴的空间直角坐标系如图:
则P(1,0,0),C(0,1,0),D(0,1,1),A(0,﹣1,1)
![]() =(﹣1,﹣1,1),
=(﹣1,﹣1,1), ![]() =(﹣1,1,0),
=(﹣1,1,0),
则平面ACD的一个法向量为 ![]() =(1,0,0),
=(1,0,0),
设 ![]() =(x,y,z)是平面PAC的法向量,
=(x,y,z)是平面PAC的法向量,
则  ,
,
令x=1,则y=1,z=2,即 ![]() =(1,1,2),
=(1,1,2),
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∵二面角P﹣AC﹣D是钝二面角,
∴二面角P﹣AC﹣D的余弦值是﹣ ![]() .
.

【解析】(1)根据面面垂直的判定定理证明PC⊥面PAB即可证明平面PAC⊥平面PAB;(2)连接OP,作OE垂直BC,建立以O为坐标原点的空间直角坐标系如图:求出平面的法向量,利用向量法进行求解即可二面角P﹣AC﹣D的余弦值.
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


科目:高中数学 来源: 题型:
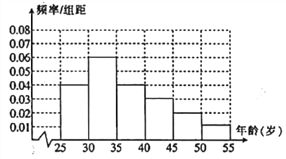
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log![]() .
.
(1)当a=1时,解不等式f(x)>1;
(2)若关于x的方程g(x)=f(x)﹣log3(ax+1)有且只有一个零点,求a的取值范围;
(3)设0<a<1,若对任意t![]() ,函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(﹣∞,+∞)上的偶函数,x1 , x2∈[0,+∞)(x1≠x2),有 ![]() ,则( )
,则( )
A.f(3)<f(1)<f(﹣2)
B.f(1)<f(﹣1)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(﹣2)<f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C,F为⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.求证:DE2=DADB. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若a,b∈R,且a+b>4,则a,b至少有一个大于2
B.若p是q的充分不必要条件,则¬p是¬q的必要不充分条件
C.若命题p:“ ![]() >0”,则¬p:“
>0”,则¬p:“ ![]() ≤0”
≤0”
D.△ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com