
【题目】如图,已知抛物线C:![]() ,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接
,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接![]() ,
,![]() 分别交抛物线于点C,D,且
分别交抛物线于点C,D,且![]() ,设
,设![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
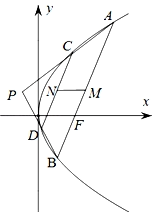
(1)求证:![]() 轴;
轴;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.
的左上方.
(1)若以![]() 为直径的圆恰好经过椭圆右焦点
为直径的圆恰好经过椭圆右焦点![]() ,求此时直线
,求此时直线![]() 的方程;
的方程;
(2)求证:![]() 的内切圆的圆心在定直线
的内切圆的圆心在定直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
②函数![]() 的最小值为2
的最小值为2
③命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
④已知双曲线![]() 过点
过点![]() ,且渐近线为
,且渐近线为![]() ,则离心率
,则离心率![]() ,其中所有正确命题的编号是:_______.
,其中所有正确命题的编号是:_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】检验中心为筛查某种疾病,需要检验血液是否为阳性,对![]() 份血液样本,有以下两种检验方式:①逐份检验,需要检验
份血液样本,有以下两种检验方式:①逐份检验,需要检验![]() 次;②混合检验,即将其中
次;②混合检验,即将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,这
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,再对这
份血液究竟哪几份为阳性,再对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为点
,采用混合检验方式,样本需要检验的总次数为点![]() .当
.当![]() 时,根据
时,根据![]() 和
和![]() 的期望值大小,讨论当
的期望值大小,讨论当![]() 取何值时,采用逐份检验方式好?
取何值时,采用逐份检验方式好?
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙、丁、戊5种在线教学软件,若某学校要从中随机选取3种作为教师“停课不停学”的教学工具,则其中甲、乙、丙至多有2种被选取的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为抛物线
为抛物线![]() 上不同的两点,且
上不同的两点,且![]() ,点
,点![]()
![]() 且
且![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)过![]() 轴上一点
轴上一点 ![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 的准线上的射影分别为
的准线上的射影分别为![]() ,
,![]() 为
为![]() 的焦点,若
的焦点,若![]() ,求
,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com