
【题目】已知函数f(x)=![]() ,g(x)=xlnx.
,g(x)=xlnx.
(Ⅰ)若函数g(x)的图象在(1,0)处的切线l与函数f(x)的图象相切,求实数k的值;
(Ⅱ)当k=0时,证明:f(x)+g(x)>0;
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(Ⅰ)根据导函数的几何意义求得函数g(x)的图象在(1,0)处的切线l的方程,将其方程与函数f(x)的解析式联立,得到关于x的一元二次方程,由条件可知此方程有一个解,判别式等于0,可求得实数k的值;(Ⅱ)证法一:当k=0时,构造函数F(x)=f(x)+g(x)=![]() ,求导判断函数F(x)在(0,+∞)上的单调性,进而得其最小值,判断最小值大于0即可。证法二:对于函数g(x)=xlnx,求导判断其单调性,可求其最小值,当k=0时,
,求导判断函数F(x)在(0,+∞)上的单调性,进而得其最小值,判断最小值大于0即可。证法二:对于函数g(x)=xlnx,求导判断其单调性,可求其最小值,当k=0时,![]() ,配方可求其最小值。进而可得f(x)+g(x)>
,配方可求其最小值。进而可得f(x)+g(x)>![]()
,可证明要证不等式。
(Ⅰ)g(x)的导数g′(x)=1+lnx,斜率为g′(1)=1,切点为(1,0),则直线l:y=x﹣1,
联立y=![]() x2+(k﹣1)x﹣k+
x2+(k﹣1)x﹣k+![]() ,可得x2+2(k﹣2)x﹣2k+5=0,
,可得x2+2(k﹣2)x﹣2k+5=0,
由l与f(x)的图象相切,可得△=4(k﹣2)2﹣4(5﹣2k)=0,解得k=1±![]() ;
;
(Ⅱ)证法一:当k=0时,F(x)=f(x)+g(x)=xlnx+![]() x2﹣x+
x2﹣x+![]() ,
,
F′(x)=lnx+x,x>0,显然F′(x)在(0,+∞)递增,
设F′(x0)=0,即lnx0+x0=0,易得x0∈(0,1),
当x∈(0,x0),F′(x)<0,F(x)递减,当x∈(x0,+∞),F′(x)>0,F(x)递增.
F(x)的最小值为F(x0),且为x0lnx0++![]() x02﹣x0+
x02﹣x0+![]() =x0(﹣x0+
=x0(﹣x0+![]() x0﹣1)+
x0﹣1)+![]()
=﹣![]() x02﹣x0+
x02﹣x0+![]() =﹣
=﹣![]() (x0+3)(x0﹣1),由x0∈(0,1),F(x0)>0,
(x0+3)(x0﹣1),由x0∈(0,1),F(x0)>0,
故F(x)>0恒成立,即f(x)+g(x)>0恒成立;
证法二:g′(x)=1+lnx,x∈(0,![]() ),g′(x)<0,g(x)递减,
),g′(x)<0,g(x)递减,
x∈(![]() ,+∞),g′(x)>0,g(x)递增,则g(x)在x=
,+∞),g′(x)>0,g(x)递增,则g(x)在x=![]() 处取得最小值﹣
处取得最小值﹣![]() ,即g(x)≥
,即g(x)≥![]() ,
,
又k=0时,f(x)=![]() x2﹣x+
x2﹣x+![]() =
=![]() (x﹣1)2+1≥1,则f(x)+g(x)>1﹣
(x﹣1)2+1≥1,则f(x)+g(x)>1﹣![]() >0恒成立;
>0恒成立;


科目:高中数学 来源: 题型:
【题目】(12分)已知函数![]() .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在![]() 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 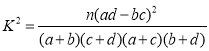 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,MN分别是边长为1的正方形ABCD的边BCCD的中点,将正方形沿对角线AC折起,使点D不在平面ABC内,则在翻折过程中,有以下结论:

①异面直线AC与BD所成的角为定值.
②存在某个位置,使得直线AD与直线BC垂直.
③存在某个位置,使得直线MN与平面ABC所成的角为45°.
④三棱锥M-ACN体积的最大值为![]() .
.
以上所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地西红柿从2月1日起开始上市.通过市场调查,得到西红柿种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:天)的数据如下表:
(单位:天)的数据如下表:
![]()
由表知,体现![]() 与
与![]() 数据关系的最佳函数模型是( )
数据关系的最佳函数模型是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知角α的顶点与原点重合,始边与x轴的正半轴重合,终边过点P(-2,-1).
(1)求cos(2α+![]() )的值;
)的值;
(2)若角β满足tanβ=2,求tan(2α+β)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com