练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

          设函数.

         （Ⅰ）求的最小值，并求使取得最小值的的集合；

         （Ⅱ）不画图，说明函数的图像可由的图象经过怎样的变化得到.

    【解析】（1）

                      

                      

    当时，，此时

    所以，的最小值为，此时x 的集合.

    (2)横坐标不变，纵坐标变为原来的倍，得；

      然后向左平移个单位，得

    【考点定位】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力，中等难度.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

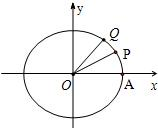    精英家教网如图，设A是单位圆和x轴正半轴的交点，P，Q是单位圆上两点，O是坐标原点，且∠AOP=
    π
    6
    ，∠AOQ=α，α∈[0，π）．
    （Ⅰ）若点Q的坐标是(
    3
    5
    ，
    4
    5
    )    ，求cos(α-
    π
    6
    )    的值；
    （Ⅱ）设函数f(α)=
    OP
    •
    OQ
    ，求f（α）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=2
    		3
    sinxcosx    ，求f（x）的最大值、最小正周期和单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•吉林二模）已知：P(
    		3
    2
    ，
    1
    2
    )    、Q(cosα，sinα)(α∈(
    π
    2
    ，π))    是坐标平面上的点，O是坐标原点．
    （Ⅰ）若点Q的坐标是(-
    3
    5
    ，m)    ，求cos(a-
    π
    6
    )    的值；
    （Ⅱ）设函数f(α)=
    OP
    •
    OQ
    ，求f（a）的值域．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年四川绵阳高中高三第二次诊断性考试文科数学试卷（解析版） 题型：解答题

    已知向量a=，b=，设函数=ab．

    （Ⅰ）求的单调递增区间；

    （Ⅱ）若将的图象向左平移个单位，得到函数的图象，求函数在区间上的最大值和最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖南省株洲市高三第五次月考文科数学试卷（解析版） 题型：解答题

    已知向量 与 共线，设函数．

    （1）求函数的周期及最大值；

    （2）已知锐角 △ABC 中的三个内角分别为 A、B、C，若有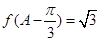，边 BC＝，，求 △ABC 的面积．

     

    查看答案和解析>>

    同步练习册答案