解:法一 f'(x)=ax
2+(b-1)x+1.
因为f(x)当x=x
1时取得极大值,当x=x
2时取得极小值.
所以f'(x)=ax
2+(b-1)x+1=0的两根为x
1,x
2,且x
1<x
2.
(Ⅰ)由题知,f'(x)=0的两个根x
1,x
2满足x
1<2<x
2<4,a>0
当且仅当
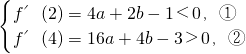
所以16a+4b>3>3(4a+2b),得-

>-1.
因为函数g(x)=ax
2+bx+1在区间(-∞,-

)上是单调减函数,
所以函数g(x)=ax
2+bx+1在区间(-∞,-1]上是单调减函数;
(Ⅱ)因为方程ax
2+(b-1)x+1=0的两个根x
1,x
2(x
1<x
2),且x
1•x
2=

>0,所以x
1,x
2同号.
又|x
1-x
2|=
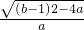
=4,所以(b-1)
2=16a
2+4a.③
若-2<x
1<0,则-2<x
1<x
2<0,则|x
1-x
2|<2,与|x
1-x
2|=4矛盾,
所以0<x
1<2,则
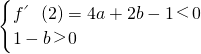
所以4a+1<2(1-b),
结合③得(4a+1)
2<4(1-b)
2=4(16a
2+4a),解得a>

或-a<

.结合a>0,得a>

.
所以2(1-b)>4a+1>

,得b<

.
所以实数b的取值范围是(-∞,

).
法二 f'(x)=ax
2+(b-1)x+1.
(Ⅰ)由题知,f'(x)=0的两个根x
1,x
2满足x
1<2<x
2<4,
当且仅当
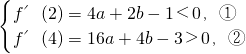
由①得,-b>2a-

.
因为a>0,所以-

>1-

.③
由
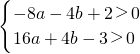
结合③,得-

>-1.
因为函数g(x)=ax
2+bx+1在区间(-∞,-

)上是单调减函数,
所以函数g(x)=ax
2+bx+1在区间(-∞,-1)上是单调减函数;
(Ⅱ)因为x
1•x
2=

>0,所以x
1,x
2同号.
由|x
1|<2,得-2<x
1<2.
若-2<x
1<0,则-2<x
1<x
2<0,则|x
1-x
2|<2,与|x
1-x
2|=4矛盾,
所以0<x
1<2,则x
2>4.
所以
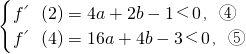
得b<

.
又因为|x
1-x
2|=
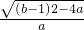
=4,所以(b-1)
2=16a
2+4a.
根据④⑤得
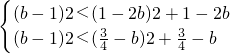
得
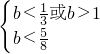
结合b<

,得b<

;
所以实数b的取值范围是(-∞,

).
分析:法一 (Ⅰ)先求导数:f'(x)=ax
2+(b-1)x+1.根据f(x)当x=x
1时取得极大值,当x=x
2时取得极小值,由题知,f'(x)=0的两个根x
1,x
2满足x
1<2<x
2<4,利用根的分布得出关于a,b的不等关系,结合二次函数的性质即可得到答案;
(Ⅱ)利用方程ax
2+(b-1)x+1=0的两个根x
1,x
2(x
1<x
2),根据根与系数的关系结合又|x
1-x
2|=4,得a,b的范围即可.
法二 (Ⅰ)先求导数f'(x)=ax
2+(b-1)x+1.由题知,f'(x)=0的两个根x
1,x
2满足x
1<2<x
2<4,利用二次方程根的分布得出a,b的不等式组,得-

>-1.最后结合二次函数的性质得出结论.
(Ⅱ)因为x
1•x
2=

>0,所以x
1,x
2同号得出两根的范围:0<x
1<2,则x
2>4.结合根的分布得出实数b的取值范围.
点评:本题是中档题,考查利用导数研究函数的单调性、函数在某点取得极值的条件,考查计算能力.

 x3+
x3+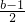 x2+x+5(a,b∈R,a>0)的定义域为R.当x=x1时取得极大值,当x=x2时取得极小值.
x2+x+5(a,b∈R,a>0)的定义域为R.当x=x1时取得极大值,当x=x2时取得极小值.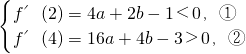
 >-1.
>-1. )上是单调减函数,
)上是单调减函数, >0,所以x1,x2同号.
>0,所以x1,x2同号.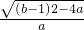 =4,所以(b-1)2=16a2+4a.③
=4,所以(b-1)2=16a2+4a.③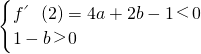 所以4a+1<2(1-b),
所以4a+1<2(1-b), 或-a<
或-a< .结合a>0,得a>
.结合a>0,得a> .
. ,得b<
,得b< .
. ).
).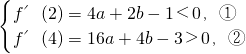
 .
. >1-
>1- .③
.③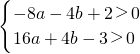 结合③,得-
结合③,得- >-1.
>-1. )上是单调减函数,
)上是单调减函数, >0,所以x1,x2同号.
>0,所以x1,x2同号.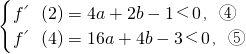 得b<
得b< .
.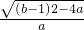 =4,所以(b-1)2=16a2+4a.
=4,所以(b-1)2=16a2+4a.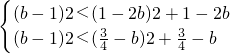 得
得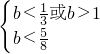 结合b<
结合b< ,得b<
,得b< ;
; ).
). >-1.最后结合二次函数的性质得出结论.
>-1.最后结合二次函数的性质得出结论. >0,所以x1,x2同号得出两根的范围:0<x1<2,则x2>4.结合根的分布得出实数b的取值范围.
>0,所以x1,x2同号得出两根的范围:0<x1<2,则x2>4.结合根的分布得出实数b的取值范围.
