练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

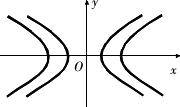
    如图，若两条双曲线的焦点在同一坐标轴上且它们的虚轴长和实轴长的比值相等，我们就称这两条双曲线是互相平行的．求经过点(2，0)且与双曲线－＝1平行的双曲线的标准方程．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

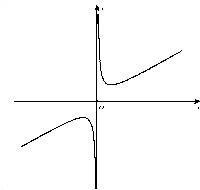    精英家教网已知等轴双曲线C的两个焦点F1、F2在直线y=x上，线段F1F2的中点是坐标原点，且双曲线经过点（3，
    3
    2
    ）．
    （1）若已知下列所给的三个方程中有一个是等轴双曲线C的方程：①x2-y2=
    27
    4
    ；②xy=9；③xy=
    9
    2
    ．请确定哪个是等轴双曲线C的方程，并求出此双曲线的实轴长；
    （2）现要在等轴双曲线C上选一处P建一座码头，向A（3，3）、B（9，6）两地转运货物．经测算，从P到A、从P到B修建公路的费用都是每单位长度a万元，则码头应建在何处，才能使修建两条公路的总费用最低？
    （3）如图，函数y=
    		3
    3
    x+
    1
    x
    的图象也是双曲线，请尝试研究此双曲线的性质，你能得到哪些结论？（本小题将按所得到的双曲线性质的数量和质量酌情给分）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

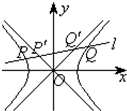    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的离心率为e，右顶点为A，左、右焦点分别为F1、F2，点E为右准线上的动点，∠AEF2的最大值为θ．
    （1）若双曲线的左焦点为F1（-4，0），一条渐近线的方程为3x-2y=0，求双曲线的方程；
    （2）求sinθ（用e表示）；
    （3）如图，如果直线l与双曲线的交点为P、Q，与两条渐近线的交点为P'、Q'，O为坐标原点，求证：
    OP
    +
    OQ
    =
    OP′
    +
    OQ′
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

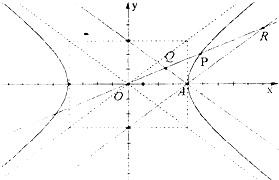    精英家教网设双曲线
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的右顶点为A，P是双曲线上异于顶点的一个动点，从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点．（如图）
    （1）证明：无论P点在什么位置，总有|
    OP
    |2=|
    OQ
    •
    OR
    |(O为坐标原点)    ；
    （2）若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积，求双曲线离心率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省高三2月月考理科数学 题型：解答题

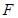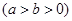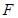    (本题满分14分)如图，已知为椭圆的右焦点，直线过点且与双曲线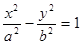的两条渐进线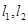分别交于点，与椭圆交于点.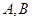

     

     

    （I）若，双曲线的焦距为4。求椭圆方程。

    （II）若（为坐标原点），，求椭圆的离心率

     

     

    查看答案和解析>>

    同步练习册答案