
分析 (1)通过对${S_n}-1=3({a_n}-1),n∈{Z^+}$变形可知Sn=3an-2,当n≥2时利用an=Sn-Sn-1计算可知an=$\frac{3}{2}$an-1,进而计算可得结论;
(2)通过(1)可知bn=(n-2)$(\frac{2}{3})^{n-1}$,通过记f(x)=(x-2)$({\frac{2}{3})}^{x-1}$并对其求导可知f(x)在区间(0,2+$\frac{1}{ln3-ln2}$)上单调递增、在区间(2+$\frac{1}{ln3-ln2}$,+∞)上单调递减,进而计算可得结论.
解答 解:(1)∵${S_n}-1=3({a_n}-1),n∈{Z^+}$,
∴Sn=3an-2,
当n≥2时,an=Sn-Sn-1=(3an-2)-(3an-1-2),
整理得:an=$\frac{3}{2}$an-1,
又∵a1=1,
∴数列{an}是首项为1、公比为$\frac{3}{2}$的等比数列,
∴an=$(\frac{3}{2})^{n-1}$;
(2)由(1)可知$({\frac{3}{2})}^{n-2}$=$(\frac{3}{2})^{({\frac{3}{2})}^{n-1}{b}_{n}}$,
∴$(\frac{3}{2})^{n-1}$bn=n-2,即bn=$\frac{n-2}{(\frac{3}{2})^{n-1}}$=(n-2)$(\frac{2}{3})^{n-1}$,
记f(x)=(x-2)$({\frac{2}{3})}^{x-1}$,则f′(x)=$({\frac{2}{3})}^{x-1}$+(x-2)$({\frac{2}{3})}^{x-1}$$ln\frac{2}{3}$=$({\frac{2}{3})}^{x-1}$[1+(x-2)$ln\frac{2}{3}$],
令f′(x)=0,即1+(x-2)$ln\frac{2}{3}$=0,
解得:x=2+$\frac{1}{ln3-ln2}$∈(4,5),
∴f(x)在区间(0,2+$\frac{1}{ln3-ln2}$)上单调递增,在区间(2+$\frac{1}{ln3-ln2}$,+∞)上单调递减,
又∵b4=(4-2)$({\frac{2}{3})}^{4-1}$=$\frac{16}{27}$,b5=(5-2)$(\frac{2}{3})^{5-1}$=$\frac{16}{27}$,
∴t≥$\frac{16}{27}$.
点评 本题考查数列的通项以及数列的单调性,考查运用导数知识判断函数的单调性,注意解题方法的积累,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
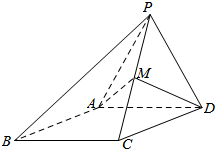 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
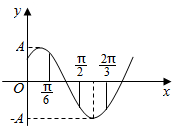 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的图象如图所示,若$f({\frac{π}{2}})=f({\frac{2π}{3}})=-f({\frac{π}{6}})$,则ω=2.
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的图象如图所示,若$f({\frac{π}{2}})=f({\frac{2π}{3}})=-f({\frac{π}{6}})$,则ω=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
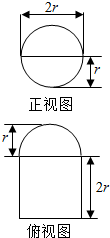 圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.
圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com