
分析 (1)利用待定系数法即可求f(x)的解析式;
(2)利用参数分离法,结合一元二次函数的性质进行求解即可.
解答 解:(1)∵f(x)是二次函数,不等式f(x)<0的解集是(0,5),
∴0,5是方程f(x)=0的两个根,且抛物线开口向上,
设f(x)=ax(x-5),a>0.
则对称轴为x=$\frac{5}{2}$,
∵f(x)在区间[-1,4]上的最大值是12,
∴当x=-1时,函数取得最大值,
此时f(-1)=6a=12,解得a=2.
则f(x)=2x(x-5).
(2)由f(x)>2m-1,得2x(x-5)>2m-1,
即2x2-10x+1>2m在区间x∈[-1,4]上恒成立,
设g(x)=2x2-10x+1,
则g(x)=2x2-10x+1=2(x-$\frac{5}{2}$)2$-\frac{23}{2}$,
∵x∈[-1,4]上,
∴当x=$\frac{5}{2}$时,函数g(x)取得最小值为$-\frac{23}{2}$,
则由$-\frac{23}{2}$>2m,得m<$-\frac{23}{4}$,
即m的取值范围是(-∞,$-\frac{23}{2}$).
点评 本题主要考查一元二次函数解析式的求解,以及一元二次函数最值的求解,利用待定系数法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
 如图,已知扇形AOP的半径为1,圆心角大小为$\frac{π}{3}$,等腰梯形ABCD是扇形AOP的内接梯形,顶点C,D分别在OP,OA上.顶点B在弧AP上,设∠AOB=θ.
如图,已知扇形AOP的半径为1,圆心角大小为$\frac{π}{3}$,等腰梯形ABCD是扇形AOP的内接梯形,顶点C,D分别在OP,OA上.顶点B在弧AP上,设∠AOB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
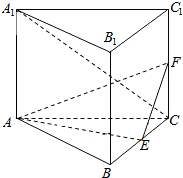 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com