
����Ŀ���������ˣ��ҵĹ�����2018�����ҹ���ӰԺ��ӳ��һ���dz���ĵ�Ӱ��¼Ƭ���ò�ӰƬ��Ҫ�������ҹ�������ķ�չ��״�ͳɾͣ�ӰƬͨ�������й����£��̻��й���ò���������й����������˹���ĸ߶ȹ�ע����ӳ�������ӰƬƱ����ͻ����3��Ԫ��ˢ�����ҹ���¼Ƭ��Ʊ����¼��ij��һ��ӰԺΪ�˽��ӰԺ�ۿ��������ˣ��ҵĹ����Ĺ��ڵ����乹������������ȡ��40����������ͳ�������
����/�� | [10��20�� | [20��30�� | [30��40�� | [40��50�� | [50��60�� | [60��70�� | [70��80�� |
���� | 6 | 8 | 12 | 6 | 4 | 2 | 2 |
��1�����������40�����������ƽ��������λ����
��2���õ�ӰԺ�������ó齱��ʽ��������Ӱ���������������ˣ��ҵĹ����ĵ�ӰƱƱ�����20Ԫ/�ţ������������ӰƱ�Ĺ��ڳ齱3�Σ��н�1�Ρ�2�Ρ�3�ηֱ��ֽ�20Ԫ��30Ԫ��60Ԫ�������ÿ���н��ĸ��ʾ�Ϊ![]() ���������3�γ齱������õĽ����ܶ����ѧ�����Ƕ���Ԫ�����������������
���������3�γ齱������õĽ����ܶ����ѧ�����Ƕ���Ԫ�����������������
���𰸡���1��ƽ����37����λ��35 ��2��11Ԫ
��������
��1��ȡÿ����м�ֵ������ƽ������ʽ��⣻ȷ������λ�����ڵ������Լ�ռ������ı��������������λ����
��2�������н��Ĵ���![]() ���Ӷ���ֲ�����X��B��3��
���Ӷ���ֲ�����X��B��3��![]() ���������н��Ĵ����뽱��Ĺ�ϵ����϶���ֲ��ĸ��ʣ���������ܶ�Y�Ŀ���ȡֵ0��20��30��60�ĸ��ʣ�����������ʽ���������.
���������н��Ĵ����뽱��Ĺ�ϵ����϶���ֲ��ĸ��ʣ���������ܶ�Y�Ŀ���ȡֵ0��20��30��60�ĸ��ʣ�����������ʽ���������.
��1����Ƶ�ʷֲ����ã�
�������40�����������ƽ����Ϊ��
![]() ��15��6+25��8+35��12+45��6+55��4+65��2+75��2����37��
��15��6+25��8+35��12+45��6+55��4+65��2+75��2����37��
��������[10��30���Ĺ�����6+8��14�ˣ�
������[30��40���Ĺ�����12�ˣ�
���������40����������������
30![]() 10��35��
10��35��
��2��������ù����н��Ĵ���X��B��3��![]() ����
����
������3�γ齱������õĽ����ܶ�Y�Ŀ���ȡֵΪ0��20��30��60��
P��Y��0����P��X��0��![]() ��
��
P��Y��20����P��X��1��=![]() ��
��
P��Y��30����P��X��2��![]() ��
��
P��Y��60����P��X��3��![]() ��
��
�������3�γ齱������õĽ����ܶ����ѧ�����ǣ�
E��X��![]() 60
60![]() 11��Ԫ����
11��Ԫ����


 ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ǡ��������ֵ��
ǡ��������ֵ��![]() .
.
(1)��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2)��֤��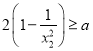 ��
��
(3)��֤�� ![]() ������
������![]() Ϊ��Ȼ�����ĵ�����.
Ϊ��Ȼ�����ĵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
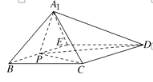
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����BAD��90����AB��2![]() ��BC��4��AD��6��E��AD�ϵĵ㣬AE��
��BC��4��AD��6��E��AD�ϵĵ㣬AE��![]() AD��P ΪBE���е㣬����ABE��BE������A1BE��λ�ã�ʹ��A1C��4����ͼ��ʾ.������BA1PD������ֵ��
AD��P ΪBE���е㣬����ABE��BE������A1BE��λ�ã�ʹ��A1C��4����ͼ��ʾ.������BA1PD������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0������f��x����|2x+2|+|x��a|����СֵΪ2��

��1����ʵ��a��ֵ��������y��f��x����ͼ��
��2����m��0��n��0����m+n��2![]() ʱ��m2+n2��f��x�����������ʵ��x��ȡֵ��Χ��
ʱ��m2+n2��f��x�����������ʵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ɽ����ɽ��![]() �����ɽ��
�����ɽ��![]() ������Ϊ
������Ϊ![]() ������б��Ϊ
������б��Ϊ![]() ������
������![]() ����б��ǰ��
����б��ǰ��![]() ��
��![]() ������Ϣ�������ʻ
������Ϣ�������ʻ![]() ����ɽ��
����ɽ��![]() ��
��

��1����ɽ�ĸ߶�![]() ��
��
��2����ɽ������һ��![]() ����
����![]() ��
��![]() �ĵ�ɽ;�У���Ա�ڵ�
�ĵ�ɽ;�У���Ա�ڵ�![]() ����������ӽ�Ϊ
����������ӽ�Ϊ![]() ������
������![]() ���߶�
���߶�![]() Ϊ
Ϊ![]() ����
����![]() Ϊ��ֵʱ���ӽ�
Ϊ��ֵʱ���ӽ�![]() ���
���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����н�ͳ����������ij�ߵ�С����2018��12����2019��11�µ������۶��ַ����ۣ���λ����Ԫ/ƽ���ף���ɢ��ͼ������ͼ��ʾ��ͼ���·ݴ���1��12�ֱ��Ӧ2018��12����2019��11�µ���Ӧ�·�.
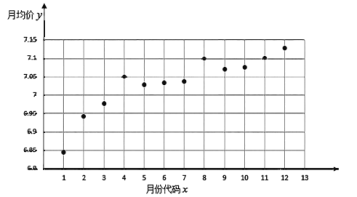
����ɢ��ͼѡ��![]() ��
��![]() ����ģ�ͽ�����ϣ��������ݴ����õ������ع鷽�̷ֱ�Ϊ
����ģ�ͽ�����ϣ��������ݴ����õ������ع鷽�̷ֱ�Ϊ![]() ��
��![]() �����õ�����һЩͳ������ֵ��
�����õ�����һЩͳ������ֵ��
|
| |
�в�ƽ���� | 0.0148557 | 0.0048781 |
��ƫ��ƽ���� | 0.069193 | |
��1�����������ָ��![]() �ж��ĸ�ģ�͵����Ч�����ã�
�ж��ĸ�ģ�͵����Ч�����ã�
��2��ijλ����������2020��5�·ݹ��������и�����![]() ƽ���Ķ��ַ���������Ϊ���ͥ������.����С������ס���ķ���֤������3�꣬�������ã�1�������Ч�����õ�ģ�ͽ���������⣺
ƽ���Ķ��ַ���������Ϊ���ͥ������.����С������ס���ķ���֤������3�꣬�������ã�1�������Ч�����õ�ģ�ͽ���������⣺
��i������ù�����Ӧ֧���Ĺ������.�����������˰�ѣ����ݾ��۾�ȷ��0.01��Ԫ/ƽ���ף�
��ii�����ù��������ò�����760��Ԫ���ʽ����С��һ���ַ����Թ�����ɹ��������������ȷ��1ƽ���ף�
��ע�������йع涨�����ַ�������Ҫ����������˰�ѣ�˰���ǰ��շ��ݵļ�˰�۸��������.����˰�۸��
���շ�ʽ���±���
����������� |
|
|
|
��˰�����ɣ���˰�� |
|
|
|
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ο���ʽ�����ָ�� .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com