练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数是函数的反函数，则               ．（要求写明自变量的取值范围）

     

    【答案】

        

    【解析】解：由y=2x-1得x-1=log2y∴x=1+log2y

    所以f-1（x）=1+log2x

    ∵f（x）=2x-1（x≥1）≥1

    ∴f-1（x）的定义域为x≥1

    故答案为1+log2x（x≥1）

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    由函数y=f（x）确定数列{an}，an=f（n），函数y=f（x）的反函数y=f-1（x）能确定数列bn，bn=f-1（n）若对于任意n∈N*都有bn=an，则称数列{bn}是数列{an}的“自反函数列”
    （1）设函数f（x）=
    px+1
    x+1
    ，若由函数f（x）确定的数列{an}的自反数列为{bn}，求an；
    （2）已知正整数列{cn}的前项和sn=
    1
    2
    （cn+
    n
    cn
    ）．写出Sn表达式，并证明你的结论；
    （3）在（1）和（2）的条件下，d1=2，当n≥2时，设dn=
    -1
    anSn2
    ，Dn是数列{dn}的前n项和，且Dn＞loga（1-2a）恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2006•宝山区二模）已知f（x）=
    10x+a10x+1
    是奇函数．
    （1）求a的值；
    （2）求f（x）的反函 数 f-1（x），判断f-1（x）的奇偶性，并给予证明；
    （3）若函数y=F（x）是以2为周期的奇函数，当x∈（-1，0）时，F（x）=f-1（x），求x∈（2，3）时F（x）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

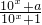    已知f（x）=数学公式是奇函数．
    （1）求a的值；
    （2）求f（x）的反函 数 f-1（x），判断f-1（x）的奇偶性，并给予证明；
    （3）若函数y=F（x）是以2为周期的奇函数，当x∈（-1，0）时，F（x）=f-1（x），求x∈（2，3）时F（x）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年长郡中学一模文）（13分）

    由函数确定数列，，函数的反函数能确定数列，，若对于任意都有，则称数列是数列的“自反函数列”.

    (I)设函数，若由函数确定的数列的自反数列为，求；

    (Ⅱ)已知正数数列的前n项和，写出表达式，并证明你的结论；

    (Ⅲ)在(I)和(Ⅱ)的条件下，，当时，设，是数列的前项和，且恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年上海市奉贤区高三（上）摸底数学试卷（理科）（解析版） 题型：解答题

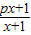    由函数y=f（x）确定数列{an}，an=f（n），函数y=f（x）的反函数y=f-1（x）能确定数列bn，bn=f-1（n）若对于任意n∈N*都有bn=an，则称数列{bn}是数列{an}的“自反函数列”
    （1）设函数f（x）=，若由函数f（x）确定的数列{an}的自反数列为{bn}，求an；
    （2）已知正整数列{cn}的前项和sn=（cn+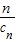）．写出Sn表达式，并证明你的结论；
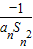    （3）在（1）和（2）的条件下，d1=2，当n≥2时，设dn=，Dn是数列{dn}的前n项和，且Dn＞loga（1-2a）恒成立，求a的取值范围．

    查看答案和解析>>

    同步练习册答案